

分析 (1)根据相似三角形的判定定理得到△AMN∽△ABC,根据相似三角形的性质列出比例式,计算即可;
(2)根据相似三角形的性质分别计算出三种情况下公共部分的面积,比较即可.
解答 解:(1)如图1,∵MN∥BC,
∴△AMN∽△ABC,
∴$\frac{MN}{BC}$=$\frac{AK}{AD}$,即$\frac{x}{6}$=$\frac{8-x}{8}$,
解得,x=$\frac{24}{7}$,即MN的长为$\frac{24}{7}$;
(2)公共部分分三种情况,
在三角形内部、一边在BC上,正方形一部分在三角形的外部,
显然在内部的面积比刚好在边上时要小,所以比较后两种情形时的面积大小,
当PQ在BC边上时,正方形MPQN与△ABC公共部分的面积y=($\frac{24}{7}$)2=$\frac{576}{49}$,
当PQ在△ABC的外部时,正方形的边长x的范围是$\frac{24}{7}$<x<6, ∵MN∥BC,
∵MN∥BC,
∴△AMN∽△ABC,
∴$\frac{MN}{BC}$=$\frac{AK}{AD}$,即$\frac{x}{6}$=$\frac{8-KD}{8}$,
解得,KD=8-$\frac{4}{3}$x,
∴公共部分的面积y=x×(8-$\frac{4}{3}$x)=-$\frac{4}{3}$x2+8x=-$\frac{4}{3}$(x-3)2+12,
当x>3时,y随x的增大而减小,
∴当x=$\frac{24}{7}$时,公共部分的面积最大,最大值是$\frac{576}{49}$,
则当x是$\frac{24}{7}$时,公共部分的面积y最大,最大值是$\frac{576}{49}$.
点评 本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD、则∠P=( )
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD、则∠P=( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
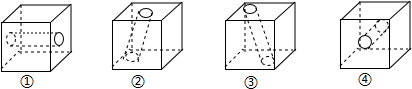
| A. | ①和④更重 | B. | ③最轻 | C. | 质量仍然一样 | D. | ②和③更重 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如表给出一个二次函数的一些取值情况:
如表给出一个二次函数的一些取值情况:| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com