
分析 (1)如图1,根据“HL”定理,即可得到Rt△ABC≌Rt△DEF;
(2)如图2,在钝角△ABC和钝角△DEF中,AB=DE,BC=EF,∠BAC=∠EDF,作BM⊥AC于M,EN⊥DF于N,先证明△ABM≌△DEN得到AM=DN,BM=EN,再证明△BCM≌Rt△EFN得到CM=FN,则CA=FD,然后根据“SSS”判断△ABC≌△DEF;
(3)画出反例图.
解答  解:(1)如果两边和其中一边所对的角对应相等,且这个角为直角,则这两个三角形全等.如图1,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理可判断Rt△ABC≌Rt△DEF;
解:(1)如果两边和其中一边所对的角对应相等,且这个角为直角,则这两个三角形全等.如图1,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理可判断Rt△ABC≌Rt△DEF;
(2)如果两边和其中一边所对的角对应相等,且这个角为钝角,则这两个三角形全等.如图2,在钝角△ABC和钝角△DEF中,AB=DE,BC=EF,∠BAC=∠EDF, 作BM⊥AC于M,EN⊥DF于N,
作BM⊥AC于M,EN⊥DF于N,
∵∠BAC=∠EDF,
∴∠BAM=∠EDN,
在△ABM和△DEN中
$\left\{\begin{array}{l}{∠M=∠N}\\{∠BAM=∠EDN}\\{AB=DE}\end{array}\right.$,
∴△ABM≌△DEN,
∴AM=DN,BM=EN,
在Rt△BCM和Rt△EFN中
$\left\{\begin{array}{l}{BC=EF}\\{BM=EN}\end{array}\right.$,
∴△BCM≌Rt△EFN,
∴CM=FN,
∴CA=FD,
∴根据“SSS”判断△ABC≌△DEF;
(3)如果两边和其中一边所对的角对应相等,且这个角为锐角,则这两个三角形不一定全等.
如图3,在△ACB和△ADB中,∠BAC=∠DAB,AB=AB,BC=BD,而△ACB与△ADB不全等.
点评 本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 棉花纤维长度x | 组中值 | 频数 |
| 0≤x<8 | 4 | 2 |
| 8≤x<16 | 12 | 2 |
| 16≤x<24 | 20 | 2 |
| 24≤x<32 | 28 | 12 |
| 32≤x<40 | 36 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将正整数按如图所示规律排列下去,若用有序实数对(m,n)表示m排,从左到右第n个数,如(4,3)表示实数9,则(10,8)表示实数是53.
将正整数按如图所示规律排列下去,若用有序实数对(m,n)表示m排,从左到右第n个数,如(4,3)表示实数9,则(10,8)表示实数是53.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
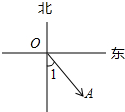 如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )
如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )| A. | 商船在海岛的北偏西50°方向 | B. | 海岛在商船的北偏西40°方向 | ||
| C. | 海岛在商船的东偏南50°方向 | D. | 商船在海岛的东偏南40°方向 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 二次函数y=ax2(a≠0)的图象的一部分如图所示,点A的坐标为(0,1).
二次函数y=ax2(a≠0)的图象的一部分如图所示,点A的坐标为(0,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com