
如图,在△ABC中,∠B、∠C的平分线BE、CD相交于F,∠ABC=42º,∠A=60º,则∠BFC=( )
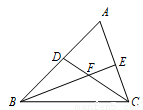
A、118º B、119º C、120º D、121º
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年浙江省江山市九年级上学期质量检测数学试卷(解析版) 题型:选择题
在比例尺为1:10000的地图上,若某建筑物在图上的面积为50cm2,则该建筑物实际占地面积为( )
A.50m2 B.5000m2 C.50000m2 D.500000m2
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(四川绵阳卷)数学(解析版) 题型:选择题
如图,要在宽为22米的九洲大道AB两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120º角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直。当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC的高度应设计为( )
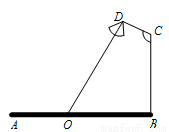
A、 米 B、
米 B、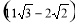 米
米
C、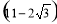 米 D、
米 D、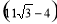 米
米
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(河南卷)数学(解析版) 题型:解答题
(11分)如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PF⊥BC于点F. 点D、E的坐标分别为(0,6),(-4,0),连接PD,PE,DE.

(1)请直接写出抛物线的解析式;
(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值. 进而猜想:对于任意一点P,PD与PF的差为定值. 请你判断该猜想是否正确,并说明理由;
(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE的周长最小时“好点”的坐标.
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(北京卷)数学(解析版) 题型:解答题
在正方形ABCD中,BD是一条对角线.点P在射线CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH、PH.

(1)若点P在线CD上,如图1,
①依题意补全图1;②判断AH与PH的数量关系与位置关系并加以证明;
(2)若点P在线CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市怀柔区中考二模数学试卷(解析版) 题型:填空题
观察下列一组坐标:(a,b),(a,c),(b,c),(b,a),(c,a),(c,b),(a,b),(a,c)…… ,它们是按一定规律排列的,那么第9个坐标是 ,第2015个坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com