Question

【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，根据图象解答下列问题：

（1）写出方程ax2+bx+c=0的两个根；

（2）写出不等式ax2+bx+c<0的解集；

（3）若方程ax2+bx+c+k=0有两个不相等的实数根，求k的取值范围．

Answer 1

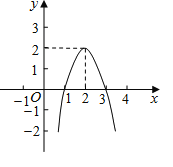
【答案】答案见解析

(1) (2) x<1或x>3 (3) K>-2

【解析】试题分析：

（1）由抛物线与轴的交点坐标可得方程的两个根；

（2）由抛物线位于轴下方部分图象所对应的自变量的取值范围可得不等式的解集；

（3）由图中信息可先求出的值，代入方程中，在根据该方程根的情况由一元二次方程根的判别式列不等式可求出的取值范围.

试题解析：

（1）如图，∵抛物线与轴两交点的横坐标分别为1和3，

∴方程的两根为；

（2）如图，∵抛物线位于轴下方部分图象所对应的自变量的取值范围为： 或，

∴不等式的解集为： 或；

（3）如图，可知点（1，0）、（3，0）在抛物线上，

∴ 抛物线的解析式为，

又∵点（2，2）在抛物线上，

∴，解得，

∴抛物线解析式为，

所以方程可化为： ，

∵该方程有两个不相等的实数根，

∴△=，解得.