
分析 (1)设$\sqrt{x}$=a,将原方程化为关于a的一元二次方程解出,再代回$\sqrt{x}$=a,求出x;
(2)设$\sqrt{{x}^{2}+3x}$=a,将原方程化为a2+a-6=0,解这个一元二次方程,再代入$\sqrt{{x}^{2}+3x}$=a中求x.
解答 解:(1)x-12+$\sqrt{x}$=0;
设$\sqrt{x}$=a,
则原方程化为:a2+a-12=0,
(a+4)(a-3)=0,
a1=-4,a2=3,
当a1=-4时,$\sqrt{x}$=-4,无实数解,
当a2=3时,$\sqrt{x}$=3,x=9,
∴原方程的解为:x=9;
(2)x2+3x+$\sqrt{{x}^{2}+3x}$=6,
设$\sqrt{{x}^{2}+3x}$=a,
则原方程化为:a2+a-6=0,
(a+3)(a-2)=0,
a1=-3,a2=2,
当a1=-3时,$\sqrt{{x}^{2}+3x}$=-3,无实数解,
当a2=2时,$\sqrt{{x}^{2}+3x}$=2,
x2+3x-4=0,
(x+4)(x-1)=0,
x1=-4,x2=1,
∴原方程的解为:x1=-4,x2=1.
点评 本题是运用换元法解可化为一元二次方程的无理方程,解方程时,把某个式子看成一个整体,用一个变量去代替它,这种方法叫换元法;此题的关键是恰当地设出新的未知数,把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
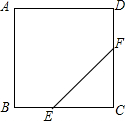 如图,在边长为12cm的正方形ABCD中,点E从点B开始沿边BC以2cm/s的速度向点C移动,点F从点C开始沿边CD以2cm/s的速度向点D移动.
如图,在边长为12cm的正方形ABCD中,点E从点B开始沿边BC以2cm/s的速度向点C移动,点F从点C开始沿边CD以2cm/s的速度向点D移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,若a、b满足方程组$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式2x+2>3(x-3)的最大整数解.
如图,在直角△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,若a、b满足方程组$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式2x+2>3(x-3)的最大整数解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
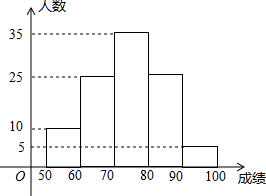 某校八年级同学进行物理知识竞赛,从中随机抽取100人的成绩进行整理,每个小组的分组标准是:50≤x<60,60≤x<70…,画出频数分布直方图如下:
某校八年级同学进行物理知识竞赛,从中随机抽取100人的成绩进行整理,每个小组的分组标准是:50≤x<60,60≤x<70…,画出频数分布直方图如下:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$=±4 | B. | ±$\sqrt{16}$=4 | C. | $\sqrt{(-4)^{2}}$=-4 | D. | $\root{3}{-27}$=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学为了了解初三年级学生体育跳绳的训练情况,从初三年级各班随机抽取了50名学生进行了1分钟跳绳的测试,并将这50名学生的测试成绩(即1分钟跳绳的次数)从低到高分成六段记为第一组到第六组,最后整理成下面的频数分布直方图:
某中学为了了解初三年级学生体育跳绳的训练情况,从初三年级各班随机抽取了50名学生进行了1分钟跳绳的测试,并将这50名学生的测试成绩(即1分钟跳绳的次数)从低到高分成六段记为第一组到第六组,最后整理成下面的频数分布直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com