
【题目】如图,正方形![]() 是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:
是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:

(1)请用两种不同的方法表示正方形![]() 的面积,并写成一个等式;
的面积,并写成一个等式;
(2)运用(1)中的等式,解决以下问题:
①已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=x2+bx+c的图象过点A(1,0)和C(0,﹣3)
(1)求这个二次函数的解析式;
(2)如果这个二次函数的图象与x轴的另一个交点为B,求线段AB的长.
(3)在这条抛物线上是否存在一点P,使△ABP的面积为8?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为A(1,0),B(3,0),探究:抛物线![]() (m为常数)交x轴于点M、N两点.
(m为常数)交x轴于点M、N两点.
(1)当m=2时.
①求出抛物线的顶点坐标及线段MN的长;
②抛物线上有一点P,使![]() ,求出点P的坐标;
,求出点P的坐标;
(2)对于抛物线![]() (m为常数).
(m为常数).
①线段MN的长是否发生变化,请说明理由.
②若该抛物线与线段AB有公共点,请直接写出m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.

(1)求出m的值并画出这条抛物线;
(2)求它与x轴的交点和抛物线顶点的坐标;
(3)x取什么值时,抛物线在x轴上方?
(4)x取什么值时,y的值随x值的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在直角三角形ABC中,∠BAC=90°,AB=AC,D为BC的中点,E为AC上一点,点G在BE上,连接DG并延长交AE于F,若∠FGE=45°.

(1)求证:BDBC=BGBE;
(2)求证:AG⊥BE;
(3)若E为AC的中点,求EF:FD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为_____cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+8与x轴,y轴分别交于点A,B,直线y=x+1与直线AB交于点C,与y轴交于点D.
x+8与x轴,y轴分别交于点A,B,直线y=x+1与直线AB交于点C,与y轴交于点D.

(1)求点C的坐标.
(2)求△BDC的面积.
(3)如图,P是y轴正半轴上的一点,Q是直线AB上的一点,连接PQ.

①若PQ∥x轴,且点A关于直线PQ的对称点A′恰好落在直线CD上,求PQ的长.
②若△BDC与△BPQ全等(点Q不与点C重合),请写出所有满足要求的点Q坐标(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
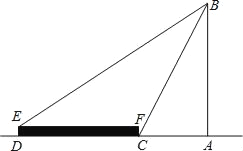
【题目】如图,在一个平台远处有一座古塔,小明在平台底部的点C处测得古塔顶部B的仰角为60°,在平台上的点E处测得古塔顶部的仰角为30°.已知平台的纵截面为矩形DCFE,DE=2米,DC=20米,求古塔AB的高(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com