
已知抛物线 与x轴交于点
与x轴交于点 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
(1)求抛物线的解析式;
(2)若抛物线向下平移k个单位后经过点(-5,6)。
①求k的值及平移后抛物线所对应函数的最小值;
②设平移后抛物线与y轴交于点D,顶点为Q,点M是平移后的抛物线上的一个动点。请探究:当点M在何处时,△MBD的而积是△MPQ面积的2倍?求出此时点M的坐标。

(1)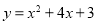 (2)①
(2)①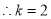 ∴对应函数的最小值是-3. ②∴点M的坐标是
∴对应函数的最小值是-3. ②∴点M的坐标是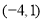 或
或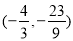
【解析】
试题分析:(1)本题考查的是二次函数的性质以及待定系数法求二次函数解析式的相关知识,我们要注意根据已知条件选择合适的关系式的设法,本题利用一般式,把两点坐标代入关系式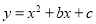 ,得到关于b、c的二元一次方程组,解方程组求出b、c的值,关系式便可得出.(2)若抛物线向下平移k个单位,
,得到关于b、c的二元一次方程组,解方程组求出b、c的值,关系式便可得出.(2)若抛物线向下平移k个单位,
也就是y值减少k,求出对应的抛物线解析式,再利用公式求出最值.②画出图形分三种情况解答.
试题解析:(1)把(-1,0),(0,3)分别代入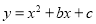
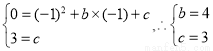
∴抛物线的解析式为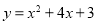
(2)①知平移后抛物线的解析式为
∵抛物线经过点(-5,6),
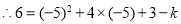 ;
;
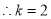
∴平移后抛物线的解析式为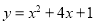
∴对应函数的最小值是-3
②由①知,BD=PQ=2,抛物线的对称轴为直线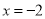 。
。
又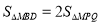
∴△MBD中BD边上的高是△MPQ中PQ边上的高的2倍。
设点M的坐标为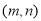 ,
,
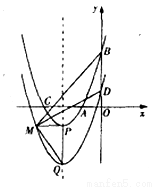
a.当点M在直线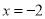 的左侧时,如图,则有
的左侧时,如图,则有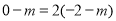 ,
,
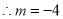 ,
,
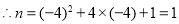 ,
,
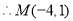 。
。
b.当点M在直线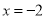 与y轴之间时,则有
与y轴之间时,则有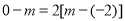
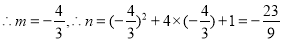 ,
,
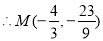
c.当点M在y轴右侧时,则有
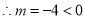 ,不合题意。
,不合题意。
∴点M的坐标是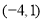 或
或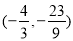
考点:1、待定系数法求二次函数解析式;2、二次函数的图象特征;3、平面直角坐标系中线段的长度的表示方法.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源:2015届北京市大兴区八年级下学期期末考试数学试卷(解析版) 题型:解答题
(根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
时间分组(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 10 | 0.2 |
0.5≤t<1 |
| 0.4 |
1≤t<1.5 | 10 | 0.2 |
1.5≤t<2 |
| 0.1 |
2≤t<2.5 | 5 |
|
合计 |
| 1 |
请你将频数分布表和频数分布直方图补充完整.

查看答案和解析>>
科目:初中数学 来源:2015届北京市丰台区八年级下学期期末考试数学试卷(解析版) 题型:选择题
下列图形中,既是中心对称图形又是轴对称图形的是( )
A.等边三角形 B.平行四边形 C.等腰梯形 D.矩形
查看答案和解析>>
科目:初中数学 来源:2015届云南省八年级上学期期末考试数学试卷(解析版) 题型:选择题
1纳米等于0.000000001米,则35纳米用科学记数法表示为( )
A、35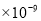 米 B、3.5×
米 B、3.5×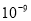 米 C、3.5×
米 C、3.5×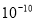 米 D、3.5×
米 D、3.5×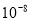 米
米
查看答案和解析>>
科目:初中数学 来源:2014年江西省吉安市吉州区九年级下学期第一次中考模拟数学试卷(解析版) 题型:解答题
如图,公园里有一块平行四边形的草坪,草坪里有一个圆形花坛,有关部门计划在草坪上修一条小路,这条小路要把草坪和花坛的面积同时平分,请在图中画出这条小路。(小路用AB表示)

查看答案和解析>>
科目:初中数学 来源:2014年北京市西城区中考二模数学试卷(解析版) 题型:解答题
如图,在四边形ABCD中,AB∥DC, DB平分∠ADC, E是CD的延长线上一点,且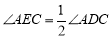 .
.
(1)求证:四边形ABDE是平行四边形.
(2)若DB⊥CB,∠BCD=60°,CD=12,作AH⊥BD于H,求四边形AEDH的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com