
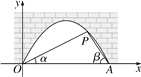
【题目】图中是抛物线型拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α,β,tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少(![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
【答案】(1)点P的坐标为![]() ;(2)水面上升1m,水面宽约为2.8m.
;(2)水面上升1m,水面宽约为2.8m.
【解析】试题分析:(1)过点P作PH⊥OA于H,如图,设PH=3x,运用三角函数可得OH=6x,AH=2x,根据条件OA=4可求出x,即可得到点P的坐标;
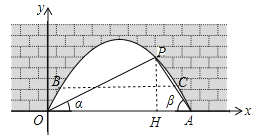
(2)若水面上升1m后到达BC位置,如图,运用待定系数法可求出抛物线的解析式,然后求出y=1时x的值,就可解决问题.
试题解析:(1)过点P作PH⊥OA于H,如图.
设PH=3x,在Rt△OHP中,∵tanα=![]() ,∴OH=6x.
,∴OH=6x.
在Rt△AHP中,∵tanβ=![]() =
=![]() ,∴AH=2x,∴OA=OH+AH=8x=4,∴x=
,∴AH=2x,∴OA=OH+AH=8x=4,∴x=![]() ,∴OH=3,PH=
,∴OH=3,PH=![]() ,∴点P的坐标为(3,
,∴点P的坐标为(3, ![]() );
);
(2)若水面上升1m后到达BC位置,如图,过点O(0,0),A(4,0)的抛物线的解析式可设为y=ax(x﹣4),∵P(3, ![]() )在抛物线y=ax(x﹣4)上,∴3a(3﹣4)=
)在抛物线y=ax(x﹣4)上,∴3a(3﹣4)=![]() ,解得a=
,解得a=![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() .
.
当y=1时, ![]() ,解得
,解得![]() ,
, ![]() ,∴BC=(
,∴BC=(![]() )﹣(
)﹣(![]() )=
)=![]() =2×1.41=2.82≈2.8.
=2×1.41=2.82≈2.8.
答:水面上升1m,水面宽约为2.8米.


科目:初中数学 来源: 题型:
【题目】如图,下列条件:①∠1=∠3,②∠2+∠4=180°,③∠4=∠5,④∠2=∠3,⑤∠6=∠2+∠3,能判断直线l1∥l2的个数是( )

A. 5B. 4C. 3D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(操作发现)
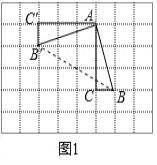
如图 1,在边长为 1 个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.现将ABC 绕点 A 按顺时针方向旋转 90°,点 B 的对应点为 B′,点 C 的对应点为 C′, 连接 BB′,如图所示则∠AB′B= .
(2)(解决问题)
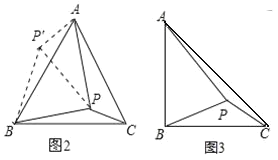
如图 2,在等边ABC 内有一点 P,且 PA=2,PB=![]() ,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
(3)(灵活运用)
如图 3,将(2)题中“在等边ABC 内有一点 P 改为“在等腰直角三角形 ABC 内有一点P”,且 BA=BC,PA=6,BP=4,PC=2,求∠BPC 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
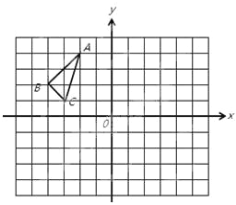
【题目】△ABC 在平面直角坐标系中的位置如图所示, 其中每个小正方形的边长为1个单位长度.
(1)△ABC 关于原点 O 的中心对称图形为△A1B1C1,写出点 A 的对应点 A1 的坐标 ;
(2)画出将△ABC 绕点O 顺时针旋转 90°得到的△A2B2C2;
(3)若 P(a,b)为△ABC 边上一点,则在△A2B2C2 中,点 P 对应的点 Q 的坐标为 .
(4)请直接写出:以 A、B、C 为顶点的平行四边形的第四个顶点 D 的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车在行驶的过程中速度往往是变化的,如图表示一辆汽车的速度随时间变化而变化的情况.
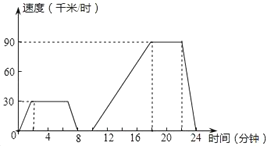
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)汽车出发8min到10min之间可能发生了什么情况?
(4)求汽车从出发后第18分钟到第22分钟行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
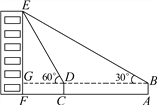
【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将下面的说理过程和理由补充完整.
已知:如图,AB∥CD,∠B=∠D,说明:BF∥DE.

解:AB∥CD.(已知)
∴∠A=∠C.( ____①___)
在△ABF和△CDE中
∵∠B=∠D=90°,(已知)
∴∠A+∠AFB=90°
∠C+___②___=90°.(直角三角形的两个锐角互余)
又∵∠A=∠C,(已证).
∴∠AFB=____③_____.(_____④_____)
∴BF∥DE.( ___⑤_____)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 ;
(2)当x 时,y随x的增大而减小;
(3)怎样移动抛物线![]() 就可以得到抛物线
就可以得到抛物线![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com