
����Ŀ��(1)���������֣�
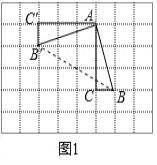
��ͼ 1���ڱ߳�Ϊ 1 ����λ���ȵ�С��������ɵ������У�ABC ������������ڸ���ϣ��ֽ�ABC �Ƶ� A ��˳ʱ�뷽����ת 90������ B �Ķ�Ӧ��Ϊ B������ C �Ķ�Ӧ��Ϊ C���� ���� BB������ͼ��ʾ���AB��B�� ��
��2����������⣩
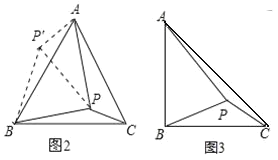
��ͼ 2���ڵȱ�ABC ����һ�� P���� PA��2��PB��![]() ��PC��1���������BPC �Ƶ� B ˳ʱ����ת 60���ó���ABP�������BPC �Ķ����� PP���ij���
��PC��1���������BPC �Ƶ� B ˳ʱ����ת 60���ó���ABP�������BPC �Ķ����� PP���ij���
��3����������ã�
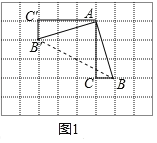
��ͼ 3������2���������ڵȱ�ABC ����һ�� P ��Ϊ���ڵ���ֱ�������� ABC ����һ��P������ BA=BC,PA��6��BP��4��PC��2�����BPC �Ķ���.
���𰸡���1����ͼ1��ʾ����������45�㣻��2����BPC��150�㣬PP�䣽![]() ����3����BPC��135��.
����3����BPC��135��.
��������
��1��������ת�ǣ���ת����ͼ�μ��ɣ�ֻҪ֤����ABB'�ǵ���ֱ�������μ��ɣ�
��2��������ת�����ʣ��ɵá�P'PB�ǵȱ������Σ��ɵȱ������ε����ʼ������PP'�ij�������PP'A����ֱ�������Σ��ɹ��ɶ������涨����֤�������ԡ�AP'B=150�㣬�Ӷ��ó����ۣ�
��3������BPC�Ƶ�B��ʱ����ת90��õ���AEB���루1�����ƣ��ɵã���EBP=��EBA+��ABP=��ABC=90�㣬�����BEP=45�㣬���ݹ��ɶ������涨�������AEP=90�㣬���ɵó����ۣ�
��ͼ1��ʾ������BB'������ABC�Ƶ�A��˳ʱ�뷽����ת90�㣬
��AB=AB'����B'AB=90�㣬���AB'B=45�㣮
�ʴ�Ϊ45�㣻
��2������ABC�ǵȱ������Σ�
���ABC=60����
����BPC�Ƶ�B˳ʱ����ת60���ó���ABP'����ͼ2��
��AP'=CP=1��BP'=BP=![]() ����PBC=��P'BA����AP'B=��BPC��
����PBC=��P'BA����AP'B=��BPC��
�ߡ�PBC+��ABP=��ABC=60����
���ABP'+��ABP=��ABC=60����
����BPP'�ǵȱ������Σ�
��PP'=![]() ����BP'P=60����
����BP'P=60����
��AP'=1��AP=2��
��AP'2+PP'2=12+��![]() ��2 =4��AP2=22=4��
��2 =4��AP2=22=4��
��AP'2+PP'2=AP2��
���AP'P=90��������PP'A��ֱ�������Σ�
���BPC=��AP'B=90��+60��=150����

��3����ͼ3������BPC�Ƶ�B��ʱ����ת90���õ���AEB��
�루1�����ƣ��ɵã�AE=PC=2��BE=BP=4����BPC=��AEB����ABE=��PBC�����EBP=��EBA+��ABP=��ABC=90����
���BEP=![]() ��180����90����=45����
��180����90����=45����
�ɹ��ɶ����ã�EP=![]() ��
��
��AE=2��AP=6��EP=![]() ��
��
��AE2+PE2=22+![]() 2=36 2=62=36��
2=36 2=62=36��
��AE2+PE2=AP2��
���AEP=90����
���BPC=��AEB=90��+45��=135����




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��D��C��F��ͬһ��ֱ���ϣ�AD=CF��AB=DE��BC=EF.
(1)��֤����ABC����DEF��
(2)����A=55�㣬��B=88�������F�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
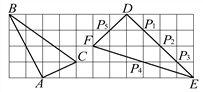
����Ŀ����ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC�͡�DEF�Ķ��㶼�ڸ���ϣ�P1��P2��P3��P4��P5�ǡ�DEF���ϵ�5����㣬�밴Ҫ��������и��⣺
(1)��֤����ABCΪֱ�������Σ�
(2)�жϡ�ABC�͡�DEF�Ƿ����ƣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y��ax+1��ͼ����M��2��3����N����3��b����
��1����һ�κ����Ľ���ʽ������ͼ�л�������ͼ��
��2����ֱ��MN��x��Ľ������꼰��MON�������
��3������ͼ��ֱ��д������xȡ��ֵʱ��һ�κ�����ֵС��3��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ύ�ڵ�A,��y�ύ�ڵ�B����ֱ��OC:y=x���ڵ�C.
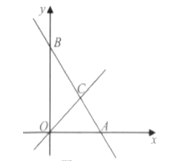
(1)��ֱ��AB����ʽΪ![]() .
.
�����C�����ꣻ
�ڸ���ͼ�������x�IJ���ʽ0<-![]() x+10<x�Ľ⼯��
x+10<x�Ľ⼯��
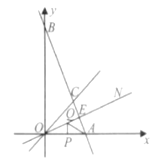
(2)����ͼ������AOC��ƽ����ON,��AB��ON,����ΪE,��OAC�����Ϊ9����OA=6��P��Q�ֱ�Ϊ�߶�OA��OE�ϵĶ��㣬����AQ��PQ,��̽��AQ+PQ�Ƿ������Сֵ?�����ڣ���������Сֵ:�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��ԶԽ���BDΪһ�߹���һ������BDEF��ʹ����һ��EF��ԭ���εĶ���C.
(1)��Rt��CBD�����ΪS1��Rt��BFC�����ΪS2��Rt��DCE�����ΪS3����S1__ __S2��S3��(���������������)
(2)д��ͼ�е��������������Σ���ѡ������һ�Խ���֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴ٽ�ѧ����������չ��ijУ��֯��չ�����Ż���ֱ������������ࡢ�����ࡢ��ѧ�༰���������ţ�Ҫ�����˲������ţ�ÿ��ֻ��ѡ��һ���Ϊ�˽�ѧ��ϲ���������Ż��ѧУ����һ�γ������飮�����ռ��������ݣ����Ƴ�����������������ͳ��ͼ�� �����ͼ���ṩ����Ϣ������������⣺
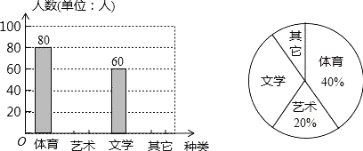
��1���˴ι������� �ˣ�
��2������ѧ����������ͳ��ͼ����ռԲ�Ľ�Ϊ �ȣ�
��3���뽫����ͳ��ͼ����������
��4������У�� 1500 ��ѧ���������ϲ�����������ŵ�ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
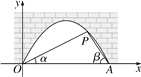
����Ŀ��ͼ�������������ţ�P����һ�����ƣ�ˮ��OA��4m����O��A�����۲�P�������Ƿֱ�Ϊ��������tan����![]() ��tan����
��tan����![]() ����OΪԭ�㣬OA����ֱ��Ϊx�Ὠ��ֱ������ϵ��
����OΪԭ�㣬OA����ֱ��Ϊx�Ὠ��ֱ������ϵ��
(1)���P�����ꣻ
(2)ˮ������1m��ˮ�������(![]() ȡ1.41�������ȷ��0.1m)?
ȡ1.41�������ȷ��0.1m)?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڰ�����С�׳���ʵ��.��ͼ1���̶���Դ���߶�MN�������Ĺ⾭��С�ף�����K�������߶�M'N'�����㹻���Ĺ̶����壨ֱ��l���ϣ�����MN// l.��֪��K�����˶������˶�·����AB��BC��CD��DA��AC��BD������������˶�ʱ��Ϊx��M'N'�ij���Ϊy����y����x�ĺ���ͼ�������ͼ2��ʾ�����K���˶�·������Ϊ�� ��
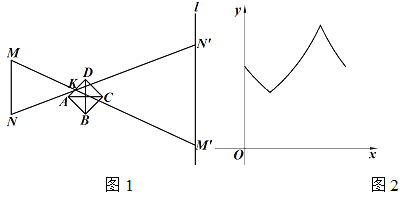
A. A��B��C��D��A B. B��C��D��A��B
C. B��C��A��D��B D. D��A��B��C��D
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com