
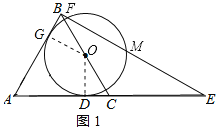
【题目】如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.
(1)求证:AB与⊙O相切;
(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.

【答案】(1)见解析;(2)2![]()
【解析】
(1)连接OD,作OG⊥AB于G,由等边三角形的性质得出∠OCD=∠OBG=∠ABC=60°,由切线的性质得出∠ODC=90°=∠OGB,证明△OBG≌△OCD得出OG=OD,即可得出结论;
(2)连接OA、OM,作OH⊥FM于H,由垂径定理得出FH=MH,证明四边形OHBG是矩形,得出OH=BG,由直角三角形的性质得出OH=BG=![]() OB=1,OG=
OB=1,OG=![]() BG=
BG=![]() ,在Rt△OMH中,由勾股定理得出MH=
,在Rt△OMH中,由勾股定理得出MH=![]() =
=![]() ,即可得出结果.
,即可得出结果.
(1)证明:连接OD,作OG⊥AB于G,如图1所示:
则∠OGB=90°,
∵△ABC为等边三角形,
∴∠OCD=∠OBG=∠ABC=60°,
∵O为BC的中点,
∴OB=OC,
∵⊙O与AC相切于点D,
∴AC⊥OD,
∴∠ODC=90°=∠OGB,
在△OBG和△OCD中,
 ,
,
∴△OBG≌△OCD(AAS),
∴OG=OD,
∴AB与⊙O相切;
(2)解:连接OA、OM,作OH⊥FM于H,如图2所示:

则∠OHB=90°,FH=MH,
∵CE=AC,AC=BC,
∴CE=BC,
∴∠CBE=∠CEB=![]() ∠ACB=30°,
∠ACB=30°,
∴∠ABE=∠ABC+∠CBE=90°,
∵∠OGB=90°,
∴四边形OHBG是矩形,
∴OH=BG,
∵△ABC是等边三角形,O为BC的中点,
∴OB=![]() BC=
BC=![]() AB=2,
AB=2,
∵∠BOG=90°﹣60°=30°,
∴OH=BG=![]() OB=1,OG=
OB=1,OG=![]() BG=
BG=![]() ,
,
在Rt△OMH中,OM=OG=![]() ,OH=1,
,OH=1,
∴MH=![]() =
=![]() ,
,
∴FM=2MH=2![]() .
.


科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育平台”是中国教育学会为方便家长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:
A.仅学生自己参与; B.家长和学生一起参与;
C.仅家长自己参与; D.家长和学生都未参与.
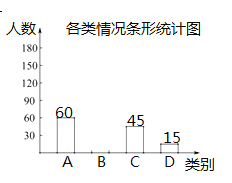
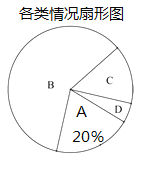
请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了________名学生;
(2)补全条形统计图,并在扇形统计图中计算![]() 类所对应扇形的圆心角的度数;
类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校1500名学生中“家长和学生都参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连接DF,则下列四个结论中,错误的是( )
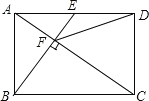
A. △AEF~△CABB. CF=2AFC. DF=DCD. tan∠CAD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店用1200元购进了A、B两种羽毛球拍.已知A种羽毛球拍进价为每副12元,B种羽毛球拍进价为每副10元.文教店在销售时A种羽毛球拍售价为每副15元,B种羽毛球拍售价为每副12元,全部售完后共获利270元.
(1)求这个文教店购进A、B两种羽毛球拍各多少副?
(2)若该文教店以原进价再次购进A、B两种羽毛球拍,且购进A种羽毛球拍的数量不变,而购进B种羽毛球拍的数量是第一次的2倍,B种羽毛球拍按原售价销售,而A种羽毛球拍降价销售.当两种羽毛球拍销售完毕时,要使再次购进的羽毛球拍获利不少于340元,A种羽毛球拍最低售价每副应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
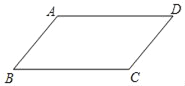
【题目】如图,点P在平行四边形ABCD的边BC上,将△ABP沿直线AP翻折,点B恰好落在边AD的垂直平分线上,如果AB=5,AD=8,tanB=![]() ,那么BP的长为_____.
,那么BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
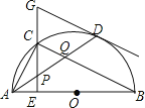
【题目】如图,在半⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是______.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三有2000名学生,为了解初三学生的体能,从人数相等的甲、乙两个班进行了抽样调查,过程如下,请补充完整.
收集数据:从甲、乙两个班各随机抽取20名学生.进行了体能测试,测试成绩(百分制)如下:
甲:78,86,74,81,75,76,87,70,75,90,75,79, 81,70, 74, 80 ,86, 69 ,83, 77.
乙:93,73,88,81,72,81,94,83,77,83,80,81,70,81,73,78,82,80,70,40.
整理、描述数据:按如下分数段整理、描述这两组样本数据:
成绩 |
|
|
|
|
|
|
甲班 | 0 | 0 | 1 | 11 | 7 | 1 |
乙班 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体能优秀,70~79分为体能良好,60~69分为体能合格,60分以下为体能不合格)
分析数据:两组样本数据的平均数、中位数、众数如下表所示:
班级 | 平均数 | 中位数 | 众数 | 优秀率 |
甲 | 78.3 | 77.5 | b | 40% |
乙 | 78 | a | 81 | c |
问题解决:
(1)表中a= ,b= ,c ;
(2)估计一下该校初三体能优秀的人数有多少人?
(3)通过以上数据的分析,你认为哪个班的学生的体能水平更高,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com