
【题目】如图,点P在平行四边形ABCD的边BC上,将△ABP沿直线AP翻折,点B恰好落在边AD的垂直平分线上,如果AB=5,AD=8,tanB=![]() ,那么BP的长为_____.
,那么BP的长为_____.
【答案】![]() 或7
或7
【解析】
①如图1,过A作AH⊥BC于H,连接DB′,设AH=4x,BH=3x,根据勾股定理得到AB=![]() =5x=5,根据旋转的性质得到AB′=AB=5,AM=DM=
=5x=5,根据旋转的性质得到AB′=AB=5,AM=DM=![]() AD=4,∠AMN=∠HNM=90°,根据勾股定理得到MB′=
AD=4,∠AMN=∠HNM=90°,根据勾股定理得到MB′=![]() =3,求得HN=MN=4,根据相似三角形的性质即可得到结论;
=3,求得HN=MN=4,根据相似三角形的性质即可得到结论;
②如图2,由①知,MN=4,MB′=3,BN=7,求得NB=NB′,推出点P与N重合,得到BP=BN=7.
①如图1,过A作AH⊥BC于H,连接DB′,

设BB′与AP交于E,
AD的垂直平分线交AD于M,BC于N,
∵tanB=![]() ,
,
∴设AH=4x,BH=3x,
∴AB=![]() =5x=5,
=5x=5,
∴x=1,
∴AH=4,BH=3,
∵将△ABP沿直线AP翻折,点B恰好落在边AD的垂直平分线MN上,
∴AB′=AB=5,AM=DM=![]() AD=4,∠AMN=∠HNM=90°,
AD=4,∠AMN=∠HNM=90°,
∴四边形AHNM是正方形,MB′=![]() =3,
=3,
∴HN=MN=4,
∴BN=7,B′N=1,
∴BB′=![]() ,
,
∴BE=![]() BB′=
BB′=![]() ,
,
∵∠BEP=∠BNB′=90°,∠PBE=∠B′BN,
∴△BPE∽△BB′N,
∴![]() ,
,
∴![]() ,
,
∴BP=![]() ;
;
②如图2,由①知,MN=4,MB′=3,BN=7,
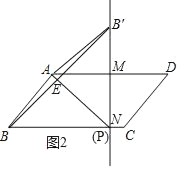
∴NB=NB′,
∴点N在BB′的垂直平分线上,
∵将△ABP沿直线AP翻折,点B恰好落在边AD的垂直平分线上,
∴点P也在BB′的垂直平分线上,
∴点P与N重合,
∴BP=BN=7,
综上所述,BP的长为![]() 或7.
或7.
故答案为:![]() 或7.
或7.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与轴交于点
与轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
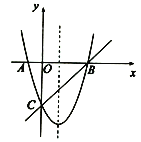
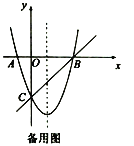
(1)求抛物线的解析式并写出其对称轴;
(2)![]() 为抛物线对称轴上一点,当
为抛物线对称轴上一点,当![]() 是以
是以![]() 为直角边的直角三角形,求
为直角边的直角三角形,求![]() 点坐标;
点坐标;
(3)若![]() 为
为![]() 轴上且位于点
轴上且位于点![]() 下方的一点,
下方的一点,![]() 为直线
为直线![]() 上的一点,在第四象限的抛物线上是否存在一点
上的一点,在第四象限的抛物线上是否存在一点![]() .使以
.使以![]() 为顶点的四边形是菱形且
为顶点的四边形是菱形且![]() 为菱形对角线?若存在,请求出
为菱形对角线?若存在,请求出![]() 点的横坐标;若不存在,请说明理由.
点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.
(1)求证:AB与⊙O相切;
(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式![]() 的实数x的所有取值的全体叫做闭区间,表示为
的实数x的所有取值的全体叫做闭区间,表示为![]() 对于一个函数,如果它的自变量x与函数值y满足:当
对于一个函数,如果它的自变量x与函数值y满足:当![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此函数的解析式;
上的“闭函数”,求此函数的解析式;
(3)若函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求实数a,b的值.
上的“闭函数”,求实数a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角![]() 的余弦值为
的余弦值为![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() ,点
,点![]() 在
在![]() 的内部,且
的内部,且![]() ,
,![]() .过点
.过点![]() 的直线
的直线![]() 分别交射线
分别交射线![]() 、射线
、射线![]() 于点
于点![]() 、
、![]() .点
.点![]() 在线段
在线段![]() 上(点
上(点![]() 不与点
不与点![]() 重合),且
重合),且![]() .
.
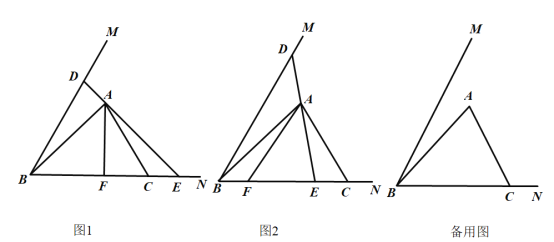
(1)如图1,当![]() 时,求
时,求![]() 的长;
的长;
(2)如图2,当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式并写出函数定义域;
的函数解析式并写出函数定义域;
(3)联结![]() ,当
,当![]() 与
与![]() 相似时,请直接写出
相似时,请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
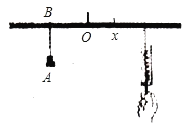
【题目】如图,小华设计了一个探索杠杆平衡的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O的右侧用一个弹簧秤向下拉木杆,改变弹簧秤与点O的距离x(单位:厘米),观察弹簧秤的示数y(单位:牛)的变化情况,实验数据记录如下:
x(单位:厘米) | … | 10 | 15 | 20 | 25 | 30 | … |
y(单位:牛) | … | 30 | 20 | 15 | 12 | 10 | … |
(1)请写出一个符合表格中数据x关于y的函数关系;
(2)当弹簧秤的示数为30牛时,弹簧秤与点O的距离是多少厘米?随着弹簧秤与O点的距离不断减小,弹簧秤的示数将发生怎样的变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF; ②点E到AB的距离是2![]() ; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
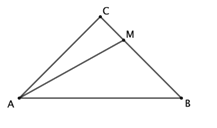
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,以点
,以点![]() 为中心,将线段
为中心,将线段![]() 顺时针旋转135°,得到线段
顺时针旋转135°,得到线段![]() ,连接
,连接![]() .
.
(1)依题意,补全图形;
(2)求证:![]() ;
;
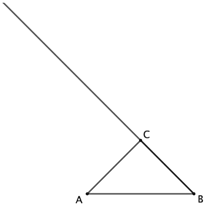
(3)点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 是点
是点![]() 关于点
关于点![]() 的对称点,写出
的对称点,写出![]() 的一个值,使得对任意的点
的一个值,使得对任意的点![]() 总有
总有![]() ,并证明.
,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com