
【题目】如图,抛物线![]() 与轴交于点
与轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
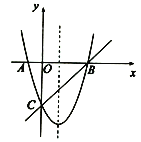
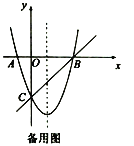
(1)求抛物线的解析式并写出其对称轴;
(2)![]() 为抛物线对称轴上一点,当
为抛物线对称轴上一点,当![]() 是以
是以![]() 为直角边的直角三角形,求
为直角边的直角三角形,求![]() 点坐标;
点坐标;
(3)若![]() 为
为![]() 轴上且位于点
轴上且位于点![]() 下方的一点,
下方的一点,![]() 为直线
为直线![]() 上的一点,在第四象限的抛物线上是否存在一点
上的一点,在第四象限的抛物线上是否存在一点![]() .使以
.使以![]() 为顶点的四边形是菱形且
为顶点的四边形是菱形且![]() 为菱形对角线?若存在,请求出
为菱形对角线?若存在,请求出![]() 点的横坐标;若不存在,请说明理由.
点的横坐标;若不存在,请说明理由.
【答案】(1)![]() ,对称轴
,对称轴![]() ;(2)点
;(2)点![]() 或
或![]() ;(3)点
;(3)点![]() .
.
【解析】
(1)将点B、C的坐标代入二次函数表达式,即可求解;
(2)分∠BCD=90![]() 、∠DBC=90
、∠DBC=90![]() 两种情况,分别求解即可;
两种情况,分别求解即可;
(3)根据CE为菱形的对角线时,PQ⊥CE,即PQ∥x轴,再根据CQ=CP得到方程组,联立即可求解.
解:(1)将点![]() 的坐标代入二次函数表达式得:
的坐标代入二次函数表达式得: ,
,
解得:![]() ,
,
故抛物线的表达式为:![]() ,
,
令![]() ,则
,则![]() 或6,则点
或6,则点![]() ,
,
则函数的对称轴![]() ;
;
(2)①当![]() 时,
时,
设BC的解析式为y=kx+b,
把B![]() 、
、![]()
![]() 代入得
代入得![]()
解得![]()
∴直线![]() 的表达式为:
的表达式为:![]() ,
,
∵BC⊥CD,
∴可设直线CD为y=-x+d
把![]()
![]() 代入y=-x+d得-6=d,
代入y=-x+d得-6=d,
∴直线![]() 的表达式为:
的表达式为:![]() ,
,
当![]() 时,
时,![]() ,故点
,故点![]() ;
;
②当![]() 时,
时,
直线![]() 的表达式为:
的表达式为:![]() ,
,
∵BD⊥CD,
∴可设直线BD为y=-x+e
把B![]() 代入y=-x+e得0=-6+e,
代入y=-x+e得0=-6+e,
∴e=6
∴直线BD的表达式为:![]() ,
,
当![]() 时,
时,![]() ,故点
,故点![]() ,
,
故点![]() 或
或![]() ;
;
(3)由题意知![]() 为菱形的对角线,
为菱形的对角线,
则![]() ,即
,即![]() 轴,
轴,
设点![]() ,则点
,则点![]() ,
,
把Q代入抛物线得![]() …①,
…①,
∵直线![]() 的表达式为:
的表达式为:![]() ,
,
∴∠CPE=45°,
∴△PCE是等腰直角三角形,
∵PE=-m,
∴![]() ,
,
∵EQ=s,CE= PE=-m
∴![]() ,
,
由题意得:![]() ,即:
,即:![]() …②
…②
联立①②并解得:![]() 或-2(舍去6)
或-2(舍去6)
故点![]() ;
;
∴点![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,以A为圆心、AB为半径画圆,与边BC交于另一点D.
,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x﹣8分别交x轴、y轴于点A、点B,抛物线y=ax2+bx(a≠0)经过点A,且顶点Q在直线AB上.
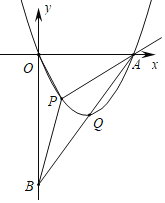
(1)求a,b的值.
(2)点P是第四象限内抛物线上的点,连结OP、AP、BP,设点P的横坐标为t,△OAP的面积为s1,△OBP的面积为s2,记s=s1+s2,试求s的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育平台”是中国教育学会为方便家长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:
A.仅学生自己参与; B.家长和学生一起参与;
C.仅家长自己参与; D.家长和学生都未参与.
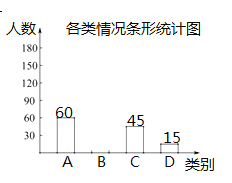
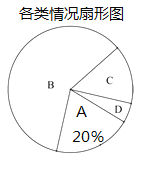
请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了________名学生;
(2)补全条形统计图,并在扇形统计图中计算![]() 类所对应扇形的圆心角的度数;
类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校1500名学生中“家长和学生都参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连接DF,则下列四个结论中,错误的是( )
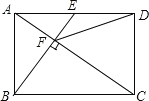
A. △AEF~△CABB. CF=2AFC. DF=DCD. tan∠CAD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在平行四边形ABCD的边BC上,将△ABP沿直线AP翻折,点B恰好落在边AD的垂直平分线上,如果AB=5,AD=8,tanB=![]() ,那么BP的长为_____.
,那么BP的长为_____.
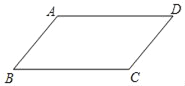
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策,这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措. 二孩政策出台后,某家庭积极响应政府号召,准备生育两个小孩(假设生男生女机会均等,且与顺序无关).
(1)该家庭生育两胎,假设每胎都生育一个小孩,求这两个小孩恰好都是女孩的概率;
(2)该家庭生育两胎,假设第一胎生育一个小孩,且第二胎生育一对双胞胎,求这三个小孩中恰好是2女1男的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com