
 如图,直角坐标系,A点是第二象限一点,AB⊥x轴于B,且C(0,2)是y轴正半轴上一点,OB-OC=2,S四边形ABOC=11.
如图,直角坐标系,A点是第二象限一点,AB⊥x轴于B,且C(0,2)是y轴正半轴上一点,OB-OC=2,S四边形ABOC=11.| 1 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| CD |
| AC |
| OC |
| CH |
| 2 |
| 4 |
| 1 |
| 2 |
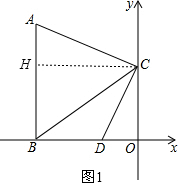 (1)∵C(0,2),OB-OC=2,
(1)∵C(0,2),OB-OC=2,| 1 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| CD |
| AC |
| OC |
| CH |
| 2 |
| 4 |
| 1 |
| 2 |
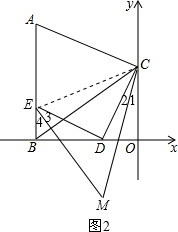 (3)结论①正确.理由如下:
(3)结论①正确.理由如下:

科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 5 |
| 7 |
| 5 |
| 7 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 7 |
| 19 |
| 20 |
| 1 |
| 6 |
| 3 |
| 8 |
| 2 |
| 3 |
| 1 |
| 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
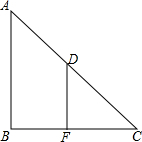 如图,某海军基地位于A处,目标B在A地正南,目标C在B处正东,A、C均与B相距200海里,小岛D位于AC的中点处,一艘军舰从A处出发,计划经B处到C处匀速巡航,一艘补给船同时从小岛D出发匀速航行(航速为军舰的一半),希望在最短时间内在军舰航线的点E处将补给物资送达军舰.
如图,某海军基地位于A处,目标B在A地正南,目标C在B处正东,A、C均与B相距200海里,小岛D位于AC的中点处,一艘军舰从A处出发,计划经B处到C处匀速巡航,一艘补给船同时从小岛D出发匀速航行(航速为军舰的一半),希望在最短时间内在军舰航线的点E处将补给物资送达军舰.查看答案和解析>>
科目:初中数学 来源: 题型:
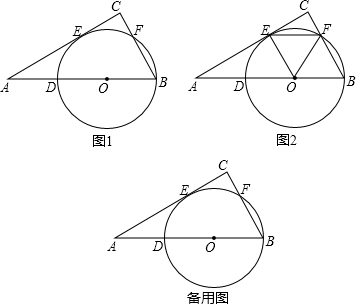 如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 17×19 |
| 1 |
| 2 |
| 1 |
| 17 |
| 1 |
| 19 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 17×19 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 17 |
| 1 |
| 19 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 17 |
| 1 |
| 19 |
| 1 |
| 2 |
| 1 |
| 19 |
| 9 |
| 19 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| x(x+3) |
| 1 |
| (x+3)(x+6) |
| 1 |
| (x+6)(x+9) |
| 1 |
| x(x+a) |
| 1 |
| (x+a)(x+2a) |
| 1 |
| (x+99a)(x+100a) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com