
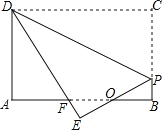
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】根据折叠的性质可得出DC=DE、CP=EP,由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP(AAS),根据全等三角形的性质可得出OE=OB、EF=BP,设EF=x,则BP=x、DF=4﹣x、BF=PC=3﹣x,进而可得出AF=1+x,在Rt△DAF中,利用勾股定理可求出x的值,再利用余弦的定义即可求出cos∠ADF的值.
根据折叠,可知:△DCP≌△DEP,
∴DC=DE=4,CP=EP.
在△OEF和△OBP中,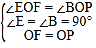 ,
,
∴△OEF≌△OBP(AAS),
∴OE=OB,EF=BP.
设EF=x,则BP=x,DF=DE﹣EF=4﹣x,
又∵BF=OB+OF=OE+OP=PE=PC,PC=BC﹣BP=3﹣x,
∴AF=AB﹣BF=1+x.
在Rt△DAF中,AF2+AD2=DF2,即(1+x)2+32=(4﹣x)2,
解得:x=![]() ,
,
∴DF=4﹣x=![]() ,
,
∴cos∠ADF=![]() ,
,
故选C.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】(3分)以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
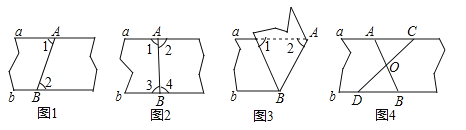
A. 如图1,展开后测得∠1=∠2
B. 如图2,展开后测得∠1=∠2且∠3=∠4
C. 如图3,测得∠1=∠2
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠CAB=∠DBA,再添加一个条件,不一定能判定△ABC≌△BAD的是( )
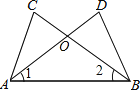
A. AC=BDB. ∠1=∠2C. AD=BCD. ∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )
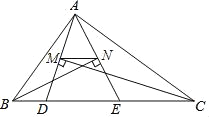
A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
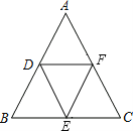
【题目】如图,在△ABC中,∠B=∠C=∠DEF,点D、E、F分别在AB、AC上,且BD=CE.求证:DE=EF.
证明:(请将下面的证明过程补充完整)
∵∠B+∠BDE+∠BED=180°(______)
∠DEF+∠FEC+∠BED=180°(______)
∠B=∠DEF(已知)
∴∠BDE=∠FEC(______)
在△BDE和△CEF中
∠B=∠C(已知)
BD=CE(______)
∠BDE=∠FEC(______)
∴△BDE≌△CEF(______)(用字母表示)
∴DE=EF(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=![]() ,OC=
,OC=![]() ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠,该班现需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)若购买的乒乓球为![]() 盒,请分别用代数式表示在两家店购买这些乒乓球和乒乓球拍时应该支付的费用;
盒,请分别用代数式表示在两家店购买这些乒乓球和乒乓球拍时应该支付的费用;
(2)当购买15盒、30盒乒乓球时,请你去办这件事,你打算去哪家商店购买,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在八年级上学期期中测试中各学科得分如下表,则下列判断正确的是( )
单元 | 语文 | 数学 | 英语 | 物理 | 历史 | 生物 | 地理 |
分数 | 85 | 80 | 92 | 80 | 85 | 95 | 85 |
A. 平均数是85B. 众数是85C. 中位数是80D. 方差是85
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com