
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点0.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什幺特殊四边形?请说明理由.
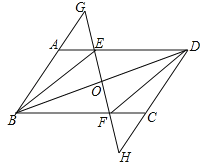
【答案】(1)证明见解析;(2)四边形BEDF是菱形.
【解析】
试题分析:(1)由平行四边形的性质得出AB=CD,∠BAE=∠DCF,由SAS证明△ABE≌△CDF即可;
(2)由平行四边形的性质得出AD∥BC,AD=BC,证出DE=BF,得出四边形BEDF是平行四边形,得出OB=OD,再由等腰三角形的三线合一性质得出EF⊥BD,即可得出四边形BEDF是菱形.
试题解析:(1)∵四边形ABCD是平行四边形,∴AB=CD,∠BAE=∠DCF,在△ABE和△CDF中,∵AB=CD,∠BAE=∠DCF,AE=CF,∴△ABE≌△CDF(SAS);
(2)四边形BEDF是菱形;理由如下:如图所示:
∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵AE=CF,∴DE=BF,∴四边形BEDF是平行四边形,∴OB=OD,∵DG=BG,∴EF⊥BD,∴四边形BEDF是菱形.


科目:初中数学 来源: 题型:
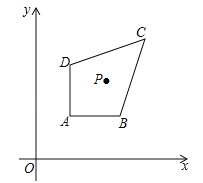
【题目】如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n﹣m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n﹣m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
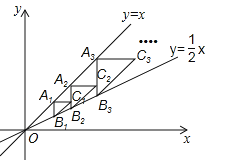
【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线![]() 于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和
于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和![]() 于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为 .(用含正整数n的代数式表示)
于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为 .(用含正整数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示, ![]() 中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。
中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。
(1)求证DA是⊙O的切线;
(2)DP的长度为多少时,∠BPC的度数最大,最大度数是多少?请说明理由。
(3)点P运动的过程中,(PB+PC)的值能否达到最小,若能,求出这个最小值,若不能,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com