
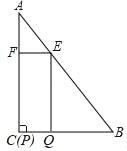
����Ŀ����ͼ���ڡ�ABC�У���A��30�㣬��C��90�㣬AB��12���ı���EFPQ�Ǿ��Σ���P���C�غϣ���Q��E��F�ֱ���BC��AB��AC�ϣ���E���A����B�����غϣ���
��1����AE��8ʱ����EF�ij���
��2����AE��x������EFPQ�����Ϊy��
����y��x�ĺ�����ϵʽ��
����xΪ��ֵʱ��y�����ֵ�����ֵ�Ƕ��٣�
��3��������EFPQ��������ʱ��������EFPQ��ÿ��1����λ���ٶ�������CB���������˶�������P�����Bʱֹͣ�˶��������˶�ʱ��Ϊt�룬����EFPQ���ABC�ص����ֵ����ΪS����S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
���𰸡���1��4����2����y=��![]() x2+3
x2+3![]() x��0��x��12������x=6ʱ��y�����ֵΪ9
x��0��x��12������x=6ʱ��y�����ֵΪ9![]() ����3��S=
����3��S=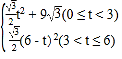
��������
(1)��EF��BC,�ɵ�![]() ,�ɴ˼��ɽ������;
,�ɴ˼��ɽ������;
(2)���ȸ��ݵ�EΪAB��һ��ó��Ա���x��ȡֵ��Χ,����30�ȵ�ֱ�������ε��������EF��AF�ij�,����Rt��ACB��,�������Ǻ������AC�ij�,����FC�ij�,���þ��ε������ʽ�����S�ĺ�����ϵʽ;
�ڰѶ��κ����Ĺ�ϵʽ�䷽���Եý���;
(3)���������ηֱ���⼴�ɽ������.
�⣺��1����Rt��ABC�У���AB=12����A=30�㣬
��BC=![]() AB=6��AC=
AB=6��AC=![]() BC=6
BC=6![]() ��
��
���ı���EFPQ�Ǿ��Σ�
��EF��BC��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��EF=4��
��2���١�AB=12��AE=x����E���A����B�����غϣ�
��0��x��12��
���ı���CDEF�Ǿ��Σ�
��EF��BC����CFE=90�㣬
���AFE=90�㣬
��Rt��AFE�У���A=30�㣬
��EF=![]() x��
x��
AF=cos30��AE=![]() x��
x��
��Rt��ACB��AB=12��
��cos30��=![]() ��
��
��AC=12��![]() =6
=6![]() ��
��
��FC=AC��AF=6![]() ��
��![]() x��
x��
��y=FCEF=![]() x��6
x��6![]() ��
��![]() x��=��
x��=��![]() x2+3
x2+3![]() x��0��x��12����
x��0��x��12����
��y=![]() x��12��x��=��
x��12��x��=��![]() ��x��6��2+9
��x��6��2+9![]() ��
��
��x=6ʱ��S�����ֵΪ9![]() ��
��
��3���ٵ�0��t��3ʱ����ͼ1�У��ص������������MFPQN��
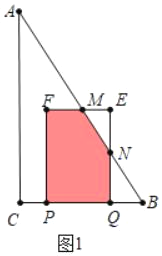
S=S����EFPQ��S��EMN=9![]() ��
��![]() t2=��
t2=��![]() t2+9
t2+9![]() ��
��
�ڵ�3��t��6ʱ���ص������ǡ�PBN��
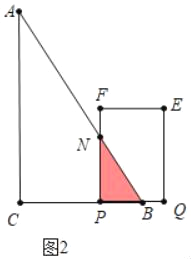
S=![]() ��6��t��2��
��6��t��2��
����������S=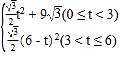


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
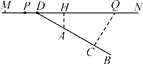
����Ŀ����ͼ��MN��ʾһ�α�ֱ�ĸܵ�·���߶�AB��ʾ�ܵ�·�Ե�һ�ž���¥����֪��A��MN�ľ���Ϊ15�ף�BA���ӳ�����MN�ཻ�ڵ�D���ҡ�BDN��30�㣬���������ڸ��ٵ�·����ʻʱ����Χ39�����ڻ��ܵ�����(XRS)��Ӱ�죮
(1)����A��MN�Ĵ��ߣ�����Ϊ��H������������Ŵ�M��N�ķ�����MN����ʻ�������������P��ʱ��������ʼӰ����һ�ŵľ���¥����ô��ʱ�������H�ľ���Ϊ�����ף�
(2)����������һ�ַ������ڸܵ�·��װ�����壬��������ʻ����Qʱ��������һ�ž���¥�ľ���QCΪ39�ף���ô������һ�ž���¥���ܵ�·��װ�ĸ�����������Ҫ�����׳���(��ȷ��1��)(�ο����ݣ�![]() ��1.7)
��1.7)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
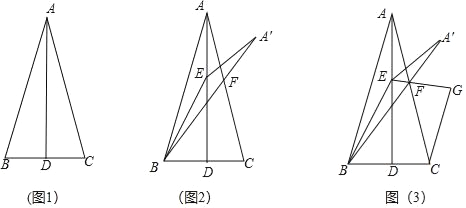
����Ŀ����֪��AD����ABC�ĸߣ���BD��CD��
��1����ͼ1����֤����BAD����CAD��
��2����ͼ2����E��AD�ϣ�����BE������ABE��BE�۵��õ���A��BE��A��B��AC�ཻ�ڵ�F����BE��BC�����BFC�Ĵ�С��
��3����ͼ3���ڣ�2���������£�����EF������C��CG��EF����EF���ӳ����ڵ�G����BF��10��EG��6�����߶�CF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����x��������������μ����ȵľ���ȡ��A1��A2��A3��A4������An���ֱ����Щ����x��Ĵ����뷴��������y��![]() ��ͼ���ཻ�ڵ�P1��P2��P3��P4����Pn���ٷֱ��P2��P3��P4����Pn��P2B1��A1P1��P3B2��A2P2��P4B3��A3P3������PnBn��1��An��1Pn��1������ֱ�ΪB1��B2��B3��B4������Bn��1������P1P2��P2P3��P3P4������Pn��1Pn���õ�һ��Rt��P1B1P2��Rt��P2B2P3��Rt��P3B3P4������Rt��Pn��1Bn��1Pn����Rt��Pn��1Bn��1Pn�����Ϊ_____��
��ͼ���ཻ�ڵ�P1��P2��P3��P4����Pn���ٷֱ��P2��P3��P4����Pn��P2B1��A1P1��P3B2��A2P2��P4B3��A3P3������PnBn��1��An��1Pn��1������ֱ�ΪB1��B2��B3��B4������Bn��1������P1P2��P2P3��P3P4������Pn��1Pn���õ�һ��Rt��P1B1P2��Rt��P2B2P3��Rt��P3B3P4������Rt��Pn��1Bn��1Pn����Rt��Pn��1Bn��1Pn�����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���Ź��ŵĽ���ͼ�������Ŷ�����������������״����ˮ��Ŀ���Ϊ10mʱ���Ŷ���ˮ��
����������5m��
��1������������ͬѧ�ǵó����ֽ���ƽ��ֱ������ϵ�ķ���������ͼ��
��ѡ��ķ�����_____�����һ��������������������B��������______���������ѡ�����е������ߵı���ʽ��
��2����Ϊ����ˮ��й����ˮ����ȱ�Ϊ6m����ˮ�����ǵĸ߶���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ��4���ֱ������1��2��3��4��С�����ǵ���״����С��ȫ��ͬ��С���ȴӿڴ����������һ��С�������Ϊx��Сӱ��ʣ�µ�3�������������һ��С�������Ϊy������ȷ���˵�P�����꣨x��y����
��1��С������������3��С��ĸ����Ƕ��٣���
��2���������б�������״ͼ����ʾ����x��yȷ���ĵ�P��x��y�����п��ܵĽ����
��3�����P��x��y���ں���y=��x+5ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
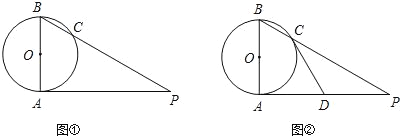
����Ŀ����֪AB�ǡ�O��ֱ����AP�ǡ�O�����ߣ�A���е㣬BP���O���ڵ�C��
��1����ͼ�٣�����P=35�������ABP�Ķ�����
��2����ͼ�ڣ���DΪAP���е㣬��֤��ֱ��CD�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
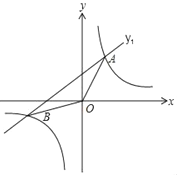
����Ŀ����ͼ����֪����������y1��![]() ��һ�κ���y2��k2x+b��ͼ���ڵ�A��2��4����B����4��m�����㣮
��һ�κ���y2��k2x+b��ͼ���ڵ�A��2��4����B����4��m�����㣮
��1����k1��k2��b��ֵ��
��2������AOB�������
��3����ֱ��д������ʽ![]() ��k2x+b�Ľ⣮
��k2x+b�Ľ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=12��BD=16��EΪAD�е㣬��P��x�����ƶ�������POEΪ���������Σ���д�����з���Ҫ��ĵ�P������ ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com