
【题目】如图,已知反比例函数y1=![]() 与一次函数y2=k2x+b的图象交于点A(2,4),B(﹣4,m)两点.
与一次函数y2=k2x+b的图象交于点A(2,4),B(﹣4,m)两点.
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() ≥k2x+b的解.
≥k2x+b的解.
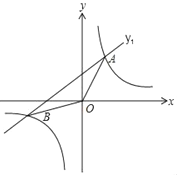
【答案】(1)k1=8,k2=1,b=2;(2)6;(3)x≤﹣4或0<x≤2.
【解析】
(1)由点A的坐标利用反比例函数图象上点的坐标特征,即可得出反比例函数解析式,再结合点B的横坐标即可得出点B的坐标,根据点A、B的坐标利用待定系数法,即可求出一次函数解析式;
(2)根据一次函数图象上点的坐标特征,即可求出一次函数图象与y轴的交点坐标,再利用分割图形法即可求出△AOB的面积;
(3)根据两函数图象的上下位置关系,即可得出不等式的解集.
(1)∵反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(2,4),B(﹣4,m),
与一次函数y=k2x+b的图象交于点A(2,4),B(﹣4,m),
∴k1=2×4=8,m=![]() =﹣2,
=﹣2,
∴点B的坐标为(﹣4,﹣2).
将A(2,4)、B(﹣4,﹣2)代入y2=k2x+b中,![]() ,
,
解得:![]() ,
,
∴k1=8,k2=1,b=2.
(2)当x=0时,y2=x+2=2,
∴直线AB与y轴的交点坐标为(0,2),
∴S△AOB=![]() ×2×4+
×2×4+![]() ×2×2=6.
×2×2=6.
(3)观察函数图象可知:
不等式![]() ≥k2x+b的解集为x≤﹣4或0<x≤2.
≥k2x+b的解集为x≤﹣4或0<x≤2.


科目:初中数学 来源: 题型:
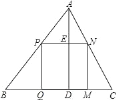
【题目】如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成一个矩形零件,使矩形PQMN的一边在BC上,其余两个顶点分别在AB、AC上.设PQ=xcm,矩形PQMN的面积为ycm2,请写出y关于x的函数表达式(并注明x的取值范围)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
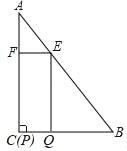
【题目】如图,在△ABC中,∠A=30°,∠C=90°,AB=12,四边形EFPQ是矩形,点P与点C重合,点Q、E、F分别在BC、AB、AC上(点E与点A、点B均不重合).
(1)当AE=8时,求EF的长;
(2)设AE=x,矩形EFPQ的面积为y.
①求y与x的函数关系式;
②当x为何值时,y有最大值,最大值是多少?
(3)当矩形EFPQ的面积最大时,将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动(当点P到达点B时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3;③a+b+c<0;④当x>1时,y随x的增大而减小;⑤2a﹣b=0;⑥b2﹣4ac>0.下列结论一定成立的是( )
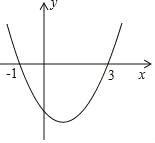
A. ①②④⑥ B. ①②③⑥ C. ②③④⑤⑥ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
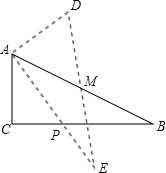
【题目】如图,在△ABC中,∠C=90°,AB=10,cosB=![]() ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
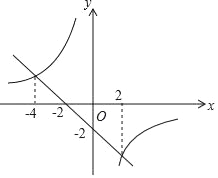
【题目】若一次函数y=kx+b与反比例函数y=![]() 的图象如图所示,则关于x的不等式kx+b﹣
的图象如图所示,则关于x的不等式kx+b﹣![]() ≤﹣2的解集为( )
≤﹣2的解集为( )
A. 0<x≤2或x≤﹣4 B. ﹣4≤x<0或x≥2
C. ![]() ≤x<0或x
≤x<0或x![]() D. x
D. x![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小芸设计的“过圆外一点作已知圆的切线”的尺规作图过程.
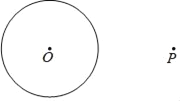
已知:⊙O及⊙O外一点P.
求作:⊙O的一条切线,使这条切线经过点P.
作法:①连接OP,作OP的垂直平分线l,
交OP于点A;
②以A为圆心,AO为半径作圆,
交⊙O于点M;
③作直线PM,则直线PM即为⊙O的切线.
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:连接OM,
由作图可知,A为OP中点,
∴OP为⊙A直径,
∴∠OMP= °,( )(填推理的依据)
即OM⊥PM.
又∵点M在⊙O上,
∴PM是⊙O的切线.( )(填推理的依据)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com