
【题目】一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P的坐标(x,y).
(1)小红摸出标有数3的小球的概率是多少?.
(2)请你用列表法或画树状图法表示出由x,y确定的点P(x,y)所有可能的结果.
(3)求点P(x,y)在函数y=﹣x+5图象上的概率.
【答案】(1)![]() ;(2)共12种情况;(3)
;(2)共12种情况;(3)![]()
【解析】
(1)根据概率公式求解;
(2)利用树状图展示所有12种等可能的结果数;
(3)利用一次函数图象上点的坐标特征得到在函数y=-x+5的图象上的结果数,然后根据概率公式求解.
解:
(1)小红摸出标有数3的小球的概率是![]() ;
;
(2)列表或树状图略:

由列表或画树状图可知,P点的坐标可能是(1,2)(1,3)(1,4)(2,1)(2,3),
(2,4)(3,1)(3,2)(3,4)(4,1)(4,2)(4,3)共12种情况,
(3)共有12种可能的结果,其中在函数y=x+5的图象上的有4种,即(1,4)(2,3)(3,2)(4,1)
所以点P(x,y)在函数y=x+5图象上的概率=![]() =
=![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
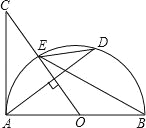
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
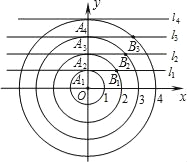
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…都在y轴上,对应的纵坐标分别为1,2,3,….直线l1,l2,l3,…分别经过点A1,A2,A3,…,且都平行于x轴.以点O为圆心,半径为2的圆与直线l1在第一象限交于点B1,以点O为圆心,半径为3的圆与直线l2在第一象限交于点B2,…,依此规律得到一系列点Bn(n为正整数),则点B1的坐标为_____,点Bn的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以点B为圆心,任意长为半径画弧,分别交AB、BC于点M、N分别以点M、N为圆心,以大于![]() MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=
MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=![]() ∠ABC;③BC=BE;④AE=BE中,一定正确的是( )
∠ABC;③BC=BE;④AE=BE中,一定正确的是( )
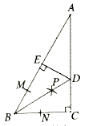
A. ①②③B. ① ② ④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
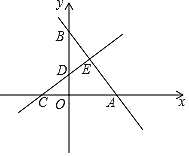
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A、点B,直线CD与x轴、y轴分别交于点C、点D,AB与CD相交于点E,线段OA、OC的长是一元二次方程x2﹣18x+72=0的两根(OA>OC),BE=5,OB=![]() OA.
OA.
(1)求点A、点C的坐标;
(2)求直线CD的解析式;
(3)在x轴上是否存在点P,使点C、点E、点P为顶点的三角形与△DCO相似?若存在,请求出点P的坐标;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
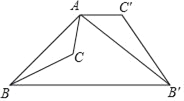
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1C1和△A2B2C2;
(2)△ABC经旋转、平移后点A的对应点分别为A1、A2,请写出点A1、A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转、平移后点P的对应点分别为P1,P2,请写出点P1、P2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2
(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求y=-2x2+5x-3函数的“旋转函数”.
小明是这样思考的:由y=-2x2+5x-3函数可知,a1=-2,b1=5,c1=-3,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面的问题:
(1)写出函数y=-2x2+5x-3的“旋转函数”;
(2)若函数y1=x2+![]() x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
(3)已知函数y=![]() (x-2)(x+3)的图像与
(x-2)(x+3)的图像与![]() 轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=
轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=![]() (x-2)(x+3)互为“旋转函数”.
(x-2)(x+3)互为“旋转函数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
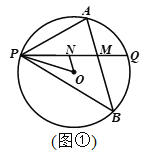
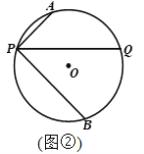
【题目】已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP. 若∠APQ=∠BPQ.
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径;
时,求⊙O的半径;
(2)如图2,选接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com