
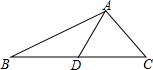
 如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,则∠ADC=50°.
如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,则∠ADC=50°. 分析 设∠ADC=α,然后根据AC=AD=DB,∠BAC=105°,表示出∠B和∠BAD的度数,最后根据三角形的内角和定理求出∠ADC的度数.
解答 解:∵AC=AD=DB,
∴∠B=∠BAD,∠ADC=∠C,
设∠ADC=α,
∴∠B=∠BAD=$\frac{α}{2}$,
∵∠BAC=105°,
∴∠DAC=105°-$\frac{α}{2}$,
在△ADC中,
∵∠ADC+∠C+∠DAC=180°,
∴2α+105°-$\frac{α}{2}$=180°,
解得:α=50°.
故答案为:50.
点评 本题考查了等腰三角形的性质:①等腰三角形的两腰相等;②等腰三角形的两个底角相等,熟练掌握等腰三角形的性质是解题的关键.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年数a | 高度h(单位:厘米) |
| 1 | 87 |
| 2 | 94 |
| 3 | 101 |
| 4 | 108 |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com