
【题目】如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论:
①b2>4ac;②ac>0; ③当x>1时,y随x的增大而减小; ④3a+c>0;⑤任意实数m,a+b≥am2+bm.
其中结论正确的序号是( )

A. ①②③ B. ①④⑤ C. ③④⑤ D. ①③⑤
【答案】D
【解析】
①∵抛物线与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴b2﹣4ac>0,即b2>4ac,故①正确;
②∵开口向下,与y轴的交点在x轴的上方,
∴a<0,c>0,
∴ac<0,故②错误;
③由图象和二次函数图象的对称轴是x=1,可得当x>1时,y随x的增大而减小,
故③正确;
④∵二次函数y=ax2+bx+c过点A (3,0),对称轴是x=1,
∴抛物线与x轴的另一交点坐标为(﹣1,0),﹣![]() =1,即b=﹣2a,
=1,即b=﹣2a,
∴当x=﹣1时,y=0,即a﹣b+c=0,
∴a+2a+c=0,
∴3a+c=0,
故④错误;
⑤∵二次函数图象的对称轴是x=1,且开口向下,
∴当x=1时,y最大,
∴任意实数m,a+b+c≥am2+bm+c.
即任意实数m,a+b≥am2+bm.
故⑤正确;
故选D.


科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=90°,点A在射线OM上运动,点B在射线ON上运动,OA>OB,点P在∠MON的平分线上,PA=PB.

(1)∠APB的大小是否发生变化?请说明理由;
(2)连接AB,点E是AB的中点,点F是OP的中点,求证:EF⊥OP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学了分式方程的解法,下面是晶晶同学的解题过程:
解方程![]()
解:整理,得:![]() ……………………………………………………第①步
……………………………………………………第①步
去分母,得:![]() ……………………………………………………………第②步
……………………………………………………………第②步
移项,得:![]() …………………………………………………………………第③步
…………………………………………………………………第③步
合并同类项,得![]() ………………………………………………………………第④步
………………………………………………………………第④步
系数化1,得:![]() …………………………………………………………………第⑤步
…………………………………………………………………第⑤步
检验:当![]() 时,
时,![]()
所以原方程的解是![]() ………………………………………………………………第⑥步
………………………………………………………………第⑥步
上述晶晶的解题辻程从第__________步开始出现错误,错误的原因是_________________.请你帮晶晶改正错误,写出完整的解题过程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且![]() ),则称点P′为点P的“k属派生点”.例如:P(1,4)属派生点为P′(1+2×4,2×1+4),即P′(9,6).
),则称点P′为点P的“k属派生点”.例如:P(1,4)属派生点为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-2,3)的“2属派生点”P′的坐标为__________.
(2) 若点P的“3属派生点”P′的坐标为(6,2),求点P的坐标;
(3) 若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .动点
.动点![]() 从点
从点![]() 出发,按
出发,按![]() 的路径运动,且速度为
的路径运动,且速度为![]() ,设出发时间为
,设出发时间为![]() .
.

(1)求![]() 的长.
的长.
(2)当![]() 时,求证:
时,求证:![]() .
.
(3)当点![]() 在
在![]() 边上运动时,若
边上运动时,若![]() 是以
是以![]() 为腰的等腰三角形,求出所有满足条件的
为腰的等腰三角形,求出所有满足条件的![]() 的值.
的值.
(4)在整个运动过程中,若![]() (
(![]() 为正整数),则满足条件的
为正整数),则满足条件的![]() 的值有________个.
的值有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
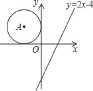
【题目】如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x﹣4上,则⊙A的半径为( )
A. ![]() B. 2 C. 4 D. 6
B. 2 C. 4 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是 ( )

A. AB=CD B. AC=BD C. ∠A=∠D D. ∠ABC=∠DCB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com