
【题目】如图,已知∠MON=90°,点A在射线OM上运动,点B在射线ON上运动,OA>OB,点P在∠MON的平分线上,PA=PB.

(1)∠APB的大小是否发生变化?请说明理由;
(2)连接AB,点E是AB的中点,点F是OP的中点,求证:EF⊥OP.
【答案】(1)∠APB的大小不会变化,理由见解析;(2)见解析
【解析】
(1)过点P作PC⊥AO于C,PD⊥OB于D,由角平分线的性质可得PC=PD,由“HL”可证Rt△ACP≌Rt△BDP,可得∠APC=∠BPD,可求∠APB=90°;
(2)由直角三角形的性质可得OE=PE=![]() AB,由等腰三角形的性质可得EF⊥OP.
AB,由等腰三角形的性质可得EF⊥OP.
解:(1)∠APB的大小不会变化,
理由如下:如图,过点P作PC⊥AO于C,PD⊥OB于D,连接OE,PE,EF,

∵PC⊥AO,PD⊥OB,∠MON=90°,
∴四边形CPDO是矩形,
∴∠CPD=90°,
∵点P在∠MON的平分线上,PC⊥AO,PD⊥OB,
∴PC=PD,且PA=PB,
∴Rt△ACP≌Rt△BDP(HL)
∴∠APC=∠BPD,
∵∠BPC+∠BPD=90°,
∴∠BPC+∠APC=90°,
∴∠APB=90°,
∴∠APB的大小不会变化.
(2)∵点E是AB的中点,∠AOB=∠APB=90°,
∴OE=![]() AB,PE=
AB,PE=![]() AB,
AB,
∴OE=PE,且点F是OP的中点,
∴EF⊥OP


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AD⊥BC于点D,BD=2,以AD为一边向右作等边三角形ADE.

(1)求△ABC的周长;
(2)判断AC、DE的位置关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF.
(1)若∠A=70°,请直接写出∠ABF的度数.
(2)若点F是CD的中点,
①求sinA的值;
②求证:S△ABE=![]() SABCD.
SABCD.
(3)设![]() =k,
=k,![]() =m,试用含k的代数式表示m.
=m,试用含k的代数式表示m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图①,在△ABC的边AB上取一点P,连接CP,可以把△ABC分成两个三角形,如果这两个三角形都是等腰三角形,我们就称点P是△ABC的边AB上的和谐点.
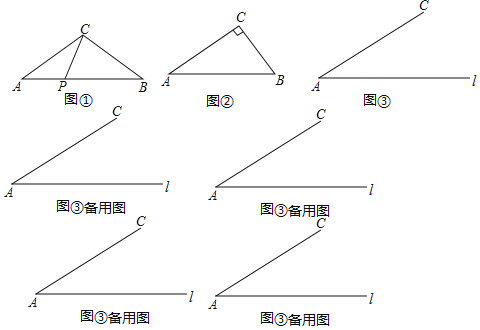
解决问题:
(1)如图②,在△ABC中,∠ACB=90°,试找出边AB上的和谐点P,并说明理由:
(2)己知∠A=36°,△ABC的顶点B在射线l上(如图③),点P是边AB上的和谐点,请在图③及备用图中画出所有符合条件的点B,用同一标记标上相等的边,并写出相应的∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5B.a:b:c=7:24:25
C.a2=b2﹣c2D.∠A=∠C﹣∠B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=5,BC=4,点P在边AB上,若△APC为以AC为腰的等腰三角形,则tan∠BCP=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上.已知α=36°,求长方形卡片的周长.
(精确到1mm,参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论:
①b2>4ac;②ac>0; ③当x>1时,y随x的增大而减小; ④3a+c>0;⑤任意实数m,a+b≥am2+bm.
其中结论正确的序号是( )

A. ①②③ B. ①④⑤ C. ③④⑤ D. ①③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com