
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)N(3,0);(3)OM=
x+4;(2)N(3,0);(3)OM=![]() AC.
AC.
【解析】试题分析:(1)由B、C的坐标,利用待定系数法可求得抛物线解析式;
(2)可设N(n,0),则可用n表示出△ABN的面积,由NM∥AC,可求得![]() ,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
(3)由N点坐标可求得M点为AB的中点,由直角三角形的性质可得OM=![]() AB,在Rt△AOB和Rt△AOC中,可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
AB,在Rt△AOB和Rt△AOC中,可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
试题解析:(1)将点B,点C的坐标分别代入y=ax2+bx+4可得
![]() ,
,
解得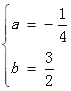 ,
,
∴二次函数的表达式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)设点N的坐标为(n,0)(﹣2<n<8),
则BN=n+2,CN=8﹣n.
∵B(﹣2,0),C(8,0),
∴BC=10,
在y=﹣![]() x2+
x2+![]() x+4中,令x=0,可解得y=4,
x+4中,令x=0,可解得y=4,
∴点A(0,4),OA=4,
∴S△ABN=![]() BNOA=
BNOA=![]() (n+2)×4=2(n+2),
(n+2)×4=2(n+2),
∵MN∥AC,
∴![]()
∴![]() ,
,
∴![]()
∵﹣![]() <0,
<0,
∴当n=3时,即N(3,0)时,△AMN的面积最大;
(3)当N(3,0)时,N为BC边中点,
∵MN∥AC,
∴M为AB边中点,
∴OM=![]() AB,
AB,
∵AB=![]() ,AC=
,AC=![]() ,
,
∴AB=![]() AC,
AC,
∴OM=![]() AC.
AC.


科目:初中数学 来源: 题型:
【题目】定义:如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(P点与A、B两点不重合).如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
(1)直接写出抛物线y=-x2+1的勾股点的坐标.
(2)如图②,已知抛物线y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1, ![]() )是抛物线的勾股点,求抛物线的函数表达式.
)是抛物线的勾股点,求抛物线的函数表达式.
(3)在(2)的条件下,点Q在抛物线上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用分式方程解决问题:元旦假期有两个小组去攀登- -座高h米的山,第二组的攀登速度是第- -组的a倍.
(1)若![]() ,两小组同时开始攀登,结果第二组比第一组早
,两小组同时开始攀登,结果第二组比第一组早![]() 到达顶峰.求两个小组的攀登速度.
到达顶峰.求两个小组的攀登速度.
(2)若第二组比第一组晚出发![]() ,结果两组同时到达顶峰,求第二组的攀登速度比第一组快多少? (用含
,结果两组同时到达顶峰,求第二组的攀登速度比第一组快多少? (用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郊区某中学学霸父母只要有时间就陪孩子一起完成家庭作业,在某天晚上,勤芬准备完成作业时:化简(![]() x2+7x+6)﹣(7x+8x2﹣4).发现系数“
x2+7x+6)﹣(7x+8x2﹣4).发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)她把“![]() ”猜成3,请你化简:(3x2+7x+6)﹣(7x+8x2﹣4);
”猜成3,请你化简:(3x2+7x+6)﹣(7x+8x2﹣4);
(2)爸爸说:“你猜错了,我看了标准答案的结果是常数.”请你通过计算说明来帮助勤芬得到原题中“![]() ”是几.
”是几.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.
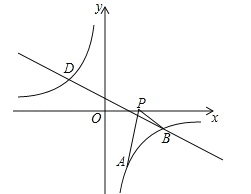
(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
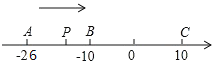
【题目】已知数轴上有A、B、C三点,分别表示有理数﹣26,﹣10,10,动点P从A出发,以每秒1个单位的速度向右移动,当P点运动到C点时运动停止,设点P移动时间为t秒。
(1)用含t的代数式表示P到点A和点C的距离:PA=_____,PC=_____.
(2)当点P运动到B点时,点Q从A出发,以每秒3个单位的速度向右运动,求t等于多少秒时P、Q两点相遇?t等于多少秒时P、Q两点相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A地仍要宣传8分钟,那么他们从B地返回学校用的时间是( )

A. 45.2分钟 B. 48分钟 C. 46分钟 D. 33分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(6,0)的直线y=kx﹣3与直线y=﹣x交于点B,点P从点O出发以每秒1个单位长度的速度向点A匀速运动.
(1)求点B的坐标;
(2)当△OPB是直角三角形时,求点P运动的时间;
(3)当BP平分△OAB的面积时,直线BP与y轴交于点D,求线段BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com