
ЁОЬтФПЁПЖЈвхЃКШчЭМЂйЃЌХзЮяЯпyЃНax2ЃЋbxЃЋc(aЁй0)гыxжсНЛгкAЃЌBСНЕуЃЌЕуPдкИУХзЮяЯпЩЯ(PЕугыAЁЂBСНЕуВЛжиКЯ)ЃЎШчЙћЁїABPЕФШ§БпТњзуAP2ЃЋBP2ЃНAB2ЃЌдђГЦЕуPЮЊХзЮяЯпyЃНax2ЃЋbxЃЋc(aЁй0)ЕФЙДЙЩЕуЃЎ
(1)жБНгаДГіХзЮяЯпyЃНЃx2ЃЋ1ЕФЙДЙЩЕуЕФзјБъЃЎ
(2)ШчЭМЂкЃЌвбжЊХзЮяЯпyЃНax2ЃЋbx(aЁй0)гыxжсНЛгкAЃЌBСНЕуЃЌЕуP(1ЃЌ ![]() )ЪЧХзЮяЯпЕФЙДЙЩЕуЃЌЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЎ
)ЪЧХзЮяЯпЕФЙДЙЩЕуЃЌЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЎ
(3)дк(2)ЕФЬѕМўЯТЃЌЕуQдкХзЮяЯпЩЯЃЌЧѓТњзуЬѕМўSЁїABQЃНSЁїABPЕФQЕу(вьгкЕуP)ЕФзјБъЃЎ

ЁОД№АИЁП(1)(0ЃЌ1)(2) yЃН-![]() x(x-4)ЃН-
x(x-4)ЃН-![]() x2ЃЋ
x2ЃЋ![]() x(3)ТњзуЬѕМўЕФЕуQга3ИіЃЌЗжБ№ЮЊ(3ЃЌ
x(3)ТњзуЬѕМўЕФЕуQга3ИіЃЌЗжБ№ЮЊ(3ЃЌ ![]() )Лђ(2ЃЋ
)Лђ(2ЃЋ![]() ЃЌЃ
ЃЌЃ ![]() )Лђ(2Ѓ
)Лђ(2Ѓ![]() ЃЌЃ
ЃЌЃ ![]() )ЃЎ
)ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮі:(1)ИљОнХзЮяЯпЙДЙЩЕуЕФЖЈвхПЩвдЧѓНт,(2)зїPGЁЭxжс,гЩЕуPЕФзјБъЧѓЕУ:AG=1,PG=![]() ,гЩШ§НЧКЏЪ§ПЩЕУ:
,гЩШ§НЧКЏЪ§ПЩЕУ: ![]() ,ПЩжЊЁЯPAG=60ЁуДгЖјЧѓЕУAB=4,МДB(4,0),Д§ЖЈЯЕЪ§ЗЈПЩЧѓНтЕУ,(3)гЩ
,ПЩжЊЁЯPAG=60ЁуДгЖјЧѓЕУAB=4,МДB(4,0),Д§ЖЈЯЕЪ§ЗЈПЩЧѓНтЕУ,(3)гЩ![]() ЧвСНИіШ§НЧаЮЭЌЕз,ПЩжЊЕуQЕНxжсЕФОрРыЮЊ
ЧвСНИіШ§НЧаЮЭЌЕз,ПЩжЊЕуQЕНxжсЕФОрРыЮЊ![]() ,МДПЩЧѓНт.
,МДПЩЧѓНт.
(1)ХзЮяЯпyЃНЃx2ЃЋ1ЕФЙДЙЩЕуЕФзјБъЮЊ(0ЃЌ1)ЃЎ
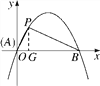
(2)ШчЭМЃЌзїPGЁЭxжсгкЕуG.ЁпЕуPЕФзјБъЮЊ(1ЃЌ![]() )ЃЌЁрAGЃН1ЃЌPGЃН
)ЃЌЁрAGЃН1ЃЌPGЃН![]() ЃЌЁрPAЃН
ЃЌЁрPAЃН![]() ЃН
ЃН![]() ЃН2.ЁпtanЁЯPABЃН
ЃН2.ЁпtanЁЯPABЃН![]() ЃН
ЃН![]() ЃЌЁрЁЯPAGЃН60Ёу.дкRtЁїPABжаЃЌABЃН
ЃЌЁрЁЯPAGЃН60Ёу.дкRtЁїPABжаЃЌABЃН![]() ЃН
ЃН![]() ЃН4ЃЌЁрЕуBЕФзјБъЮЊ(4ЃЌ0)ЃЎ
ЃН4ЃЌЁрЕуBЕФзјБъЮЊ(4ЃЌ0)ЃЎ
ЩшyЃНax(xЃ4)ЃЌНЋЕуP(1ЃЌ![]() )ДњШыЕУaЃНЃ
)ДњШыЕУaЃНЃ![]() ЃЌЁрyЃНЃ
ЃЌЁрyЃНЃ![]() x(xЃ4)ЃНЃ
x(xЃ4)ЃНЃ![]() x2ЃЋ
x2ЃЋ![]() x.
x.
(3)ЂйЕБЕуQдкxжсЩЯЗНЪБЃЌгЩSЁїABQЃНSЁїABPжЊЕуQЕФзнзјБъЮЊ![]() ЃЌдђгаЃ
ЃЌдђгаЃ![]() x2ЃЋ
x2ЃЋ![]() xЃН
xЃН![]() ЃЌНтЕУx1ЃН3ЃЌx2ЃН1(ВЛЗћКЯЬтвтЃЌЩсШЅ)ЃЌЁрЕуQЕФзјБъЮЊ(3ЃЌ
ЃЌНтЕУx1ЃН3ЃЌx2ЃН1(ВЛЗћКЯЬтвтЃЌЩсШЅ)ЃЌЁрЕуQЕФзјБъЮЊ(3ЃЌ![]() )ЃЎ
)ЃЎ
ЂкЕБЕуQдкxжсЯТЗНЪБЃЌгЩSЁїABQЃНSЁїABPжЊЕуQЕФзнзјБъЮЊЃ![]() ЃЌдђгаЃ
ЃЌдђгаЃ![]() x2ЃЋ
x2ЃЋ![]() xЃНЃ
xЃНЃ![]() ЃЌНтЕУx1ЃН2ЃЋ
ЃЌНтЕУx1ЃН2ЃЋ![]() ЃЌx2ЃН2Ѓ
ЃЌx2ЃН2Ѓ![]() ЃЌЁрЕуQЕФзјБъЮЊ(2ЃЋ
ЃЌЁрЕуQЕФзјБъЮЊ(2ЃЋ![]() ЃЌЃ
ЃЌЃ![]() )Лђ(2Ѓ
)Лђ(2Ѓ![]() ЃЌЃ
ЃЌЃ![]() )ЃЎ
)ЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуQга3ИіЃЌЗжБ№ЮЊ(3ЃЌ![]() )Лђ(2ЃЋ
)Лђ(2ЃЋ![]() ЃЌЃ
ЃЌЃ![]() )Лђ(2Ѓ
)Лђ(2Ѓ![]() ЃЌЃ
ЃЌЃ![]() )ЃЎ
)ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§жсЩЯЕуAБэЪОЕФЪ§ЮЊ6ЃЌBЪЧЪ§жсЩЯдкзѓВрЕФвЛЕуЃЌЧвAЃЌBСНЕуМфЕФОрРыЮЊ10ЁЃЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы6ИіЕЅЮЛГЄЖШЕФЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊt![]() УыЁЃ
УыЁЃ
![]()
ЃЈ1ЃЉЪ§жсЩЯЕуBБэЪОЕФЪ§ЪЧ______ЃЛЕБЕуPдЫЖЏЕНABЕФжаЕуЪБЃЌЫќЫљБэЪОЕФЪ§ЪЧ_____ЁЃ
ЃЈ2ЃЉЖЏЕуQДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌШєЕуPЁЂQЭЌЪБГіЗЂЃЌЧѓЃК
ЂйЕБЕуPдЫЖЏЖрЩйУыЪБЃЌЕуPзЗЩЯЕуQЃП
ЂкЕБЕуPдЫЖЏЖрЩйУыЪБЃЌЕуPгыЕуQМфЕФОрРыЮЊ8ИіЕЅЮЛГЄЖШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЯТСаЭМАИОљЪЧГЄЖШЯрЭЌЕФЛ№ВёАДвЛЖЈЕФЙцТЩЦДДюЖјГЩЃКЕк1ИіЭМАИаш7ИљЛ№ВёЃЌЕк2ИіЭМАИаш13ИљЛ№ВёЃЌЁЃЌвРДЫЙцТЩЃЌЕк11ИіЭМАИашЃЈ ЃЉИљЛ№ВёЃЎ

A. 156 B. 157 C. 158 D. 159
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
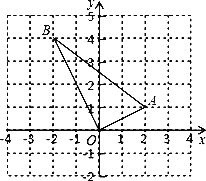
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЁїOABЃЌЕуOЮЊдЕуЃЌЕуAЁЂBЕФзјБъЗжБ№ЪЧ(2ЃЌ1)ЁЂ(Љ2ЃЌ4)ЃЎ
(1)ШєЕуAЁЂBЖМдквЛДЮКЏЪ§y=kx+bЭМЯѓЩЯЃЌЧѓkЃЌbЕФжЕЃЛ
(2)ЧѓЁїOABЕФБпABЩЯЕФжаЯпЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЮЊУРЛЏЛЗОГЃЌФГаЃМЦЛЎдквЛПщГЄЮЊ60УзЃЌПэЮЊ40УзЕФГЄЗНаЮПеЕиЩЯаоНЈвЛИіГЄЗНаЮЛЈЦдЃЌВЂНЋЛЈЦдЫФжмгрЯТЕФПеЕиаоНЈГЩЭЌбљПэЕФЭЈЕРЃЌЩшЭЈЕРПэЮЊaУзЃЎ
ЃЈ1ЃЉгУКЌaЕФЪНзгБэЪОЛЈЦдЕФУцЛ§ЃЛ
ЃЈ2ЃЉШчЙћЭЈЕРЫљеМУцЛ§ЪЧећИіГЄЗНаЮПеЕиУцЛ§ЕФ![]() ЃЌЧѓГіДЫЪБЭЈЕРЕФПэЃЎ
ЃЌЧѓГіДЫЪБЭЈЕРЕФПэЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкОиаЮABCDжа,AB=8ЃЌAD=6,ЕуEЮЊABЩЯвЛЕу,AE=2![]() ,ЕуFдкADЩЯ,НЋЁїAEFбиEFелЕў,ЕБелЕўКѓЕуAЕФЖдгІЕуA'ЧЁКУТфдкBCЕФДЙжБЦНЗжЯпЩЯЪБ,елКлEFЕФГЄЮЊ__________
,ЕуFдкADЩЯ,НЋЁїAEFбиEFелЕў,ЕБелЕўКѓЕуAЕФЖдгІЕуA'ЧЁКУТфдкBCЕФДЙжБЦНЗжЯпЩЯЪБ,елКлEFЕФГЄЮЊ__________

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРюУїзМБИНјааШчЯТВйзїЪЕбщЃЌАбвЛИљГЄ40 cmЕФЬњЫПМєГЩСНЖЮЃЌВЂАбУПЖЮЪзЮВЯрСЌИїЮЇГЩвЛИіе§ЗНаЮЃЎ
(1)вЊЪЙетСНИіе§ЗНаЮЕФУцЛ§жЎКЭЕШгк58 cm2ЃЌРюУїгІИУдѕУДМєетИљЬњЫПЃП
(2)РюУїШЯЮЊетСНИіе§ЗНаЮЕФУцЛ§жЎКЭВЛПЩФмЕШгк48 cm2ЃЌФуШЯЮЊЫћЕФЫЕЗЈе§ШЗТ№ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦЙХвЧђЪЧЮвЙњЕФЙњЧђЃЌвВЪЧЪРНчЩЯСїааЕФЧђРрЬхг§ЯюФП.ЮвЙњЦЙХвЧђУћНЋгыЦфЖдгІЩэИпШчЯТБэЫљЪОЃК
ЦЙХвЧђУћНЋ | СѕЪЋіЉ | ЕЫбЧЦМ | Азбю | ЖЁФў | ГТУЮ | ЫягБЩЏ | вІбх |
ЩэИпЃЈ | 160 | 155 | 171 | 173 | 163 | 160 | 175 |
етаЉЦЙХвЧђУћНЋЩэИпЕФжаЮЛЪ§КЭжкЪ§ЪЧЃЈ ЃЉ
A.160ЃЌ163B.173ЃЌ175C.163ЃЌ160D.172ЃЌ160
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§y=ax2+bx+4ЕФЭМЯѓгыxжсНЛгкЕуBЃЈ-2ЃЌ0ЃЉЃЌЕуCЃЈ8ЃЌ0ЃЉЃЌгыyжсНЛгкЕуAЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§y=ax2+bx+4ЕФБэДяЪНЃЛ
ЃЈ2ЃЉСЌНгACЃЌABЃЌШєЕуNдкЯпЖЮBCЩЯдЫЖЏЃЈВЛгыЕуBЃЌCжиКЯЃЉЃЌЙ§ЕуNзїNMЁЮACЃЌНЛABгкЕуMЃЌЕБЁїAMNУцЛ§зюДѓЪБЃЌЧѓNЕуЕФзјБъЃЛ
ЃЈ3ЃЉСЌНгOMЃЌдкЃЈ2ЃЉЕФНсТлЯТЃЌЧѓOMгыACЕФЪ§СПЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com