练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

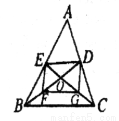
    如图，△ABC的中线BD、CE交于点O，F、G分别是BO、CO的中点。

    求证：四边形EFGD为平行四边形。

     

     

    见解析.

    【解析】

    试题分析：根据三角形中位线定理可得ED∥BC，DE=CB，FG∥CB，FG=1BC，进而得到ED=FG，DE∥FG，然后根据平行四边形的判定定理：一组对边平行且相等的四边形是平行四边形．

    试题解析：：∵BD、CE为△ABC的中线，

    ∴ED为△ABC的中位线，

    ∴ED∥BC，DE=CB，

    ∵F，G分别是BO、CO的中点，

    ∴FG是△BOC的中位线，

    ∴FG∥CB，FG= BC，

    ∴ED=FG，DE∥FG，

    ∴四边形EFGD为平行四边形.

    考点：平行四边形的判定；三角形中位线定理

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2015届江西省高安市八年级下学期期末考试数学试卷（解析版） 题型：计算题

    ﹣2+3﹣（2﹣2）

     

    查看答案和解析>>

    科目：初中数学 来源：2015届江西省八年级下学期第一次月考数学试卷（解析版） 题型：解答题

    求证：等腰三角形底边上的中点到两腰上的距离相等.(要求画图，写已知，求证和证明)

     

    查看答案和解析>>

    科目：初中数学 来源：2015届江西省八年级下学期第一次月考数学试卷（解析版） 题型：选择题

    如图所示，△ABC与△BDE都是等边三角形，AB<BD．若△ABC不动，将△BDC绕B点旋转，则在旋转过程中，AE与CD的大小关系为( )

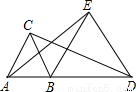
    A．AE＝CD B．AE>CD C AE<CD D．无法确定

     

    查看答案和解析>>

    科目：初中数学 来源：2015届江西省吉安市六校八年级下学期联考数学试卷（解析版） 题型：解答题

    某商场销售甲、乙两种品牌的智能手机，这两种手机的进价和售价如下表所示：

     

    甲

    乙

    进价（元/部）

    4000

    2500

    售价（元/部）

    4300

    3000

     

    该商场计划购进两种手机若干部，共需15.5万元，预计全部销售后可获毛利润共2.1万元，［毛利润＝（售价－进价）×销售量］

    （1）该商场计划购进甲、乙两种手机各多少部？

    （2）通过商场调研，该商场决定在原计划的基础上，减少甲种手机的购进数量，增加乙种手机的购进数量，已知乙种手机增加数量是甲种手机减少的数量的2倍，而且用于购进这两种手机的总资金不超过16万元，该商场怎样进货，使全部销售后获得的毛利润最大？并求出最大毛利润。

     

    查看答案和解析>>

    科目：初中数学 来源：2015届江西省吉安市六校八年级下学期联考数学试卷（解析版） 题型：填空题

    等腰三角形的周长18cm，其中一边长为8cm，则底边长为 cm．

     

    查看答案和解析>>

    科目：初中数学 来源：2015届江西省吉安市六校八年级下学期联考数学试卷（解析版） 题型：填空题

    因式分【解析】
    ＝_____________。

     

    查看答案和解析>>

    科目：初中数学 来源：2015届江苏省八年级下学期期中联考数学试卷（解析版） 题型：填空题

    若顺次连接四边形各边中点组成的四边形是菱形，则原来的四边形是 的四边形．

     

    查看答案和解析>>

    科目：初中数学 来源：2015届江苏省苏州市相城区八年级下学期期末考试数学试卷（解析版） 题型：选择题

    分式的值为0，则（ ）

    A．x＝－2 B．x＝±2 C．x＝2 D．x＝0

     

    查看答案和解析>>

    同步练习册答案