
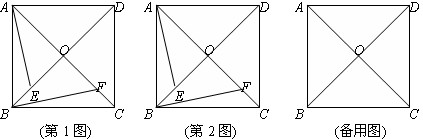
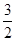 .
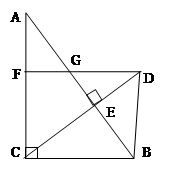
.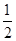 AC,则CE=
AC,则CE=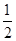 CD,即AB是CE的垂直平分线,则BC=BD=1.再根据直角三角形的性质进一步求得AB、BE的长,则AE=AB-BE,结合(1)中的全等三角形,知DF=AE.
CD,即AB是CE的垂直平分线,则BC=BD=1.再根据直角三角形的性质进一步求得AB、BE的长,则AE=AB-BE,结合(1)中的全等三角形,知DF=AE.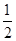 AC=
AC=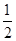 CD.
CD.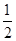 BC=
BC=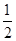 BD=
BD=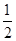 .
.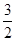 .
.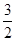 .
.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.有一锐角和一边对应相等的两个直角三角形全等 |
| B.有两边对应相等的两个直角三角形全等 |
| C.有两角对应相等,且有一条公共边的两个直角三角形全等 |
| D.有两角和一边对应相等的两个直角三角形全等 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
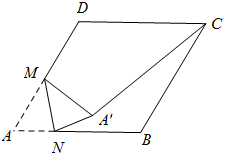
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF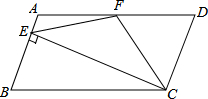
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.8米 | B.10米 | C.12米 | D.14米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com