【题目】已知m是正实数，关于x的方程2x2﹣mx﹣30=0的两个根为x1、x2，且5x1+3x2=0，在直角坐标系中，抛物线y=mx2+（4+k）x+k与x轴有_____个交点．
【答案】1或2．
【解析】
由一元二次方程方程根与系数的关系可知x1+x2=
，由因为5x1+3x2=0，从而x1=﹣
，由求根公式可求x=
，进而得到﹣=
，求出m的值后，根据根的判别式解答即可.
∵关于x的方程2x2﹣mx﹣30=0的两个根为x1、x2，
∴x1+x2=，
∵5x1+3x2=0，
∴3x1+3x2+2x1=0，
3×+2x1=0，
x1=﹣，x=，
∵m＞0，
∴﹣=，
﹣4m=﹣
，
解得：m=±4，
∴m=4，
△=（4+k）2﹣4mk=16+8k+k2﹣16k=（k﹣4）2，
当k=4时，△=0，抛物线y=mx2+（4+k）x+k与x轴有1个交点．
当k≠4时，△＞0，抛物线y=mx2+（4+k）x+k与x轴有2个交点．
故答案为：1或2．
科目：初中数学 来源： 题型：
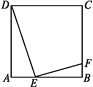
【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“绿水青山就是金山银山”，随着生活水平的提高人们对饮水品质的需求越来越高，岳阳市槐荫公司根据市场需求代理
，
两种型号的净水器，每台型净水器比每台型净水器进价多
元，用
万元购进型净水器与用
万元购进型净水器的数量相等
（1）求每台型、型净水器的进价各是多少元？
（2）槐荫公司计划购进，两种型号的共
台进行试销，，购买资金不超过
万元．试求最多可以购买型净水器多少台？
查看答案和解析>>
科目：初中数学 来源： 题型：
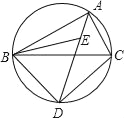
【题目】如图：△ABC是圆的内接三角形，∠BAC与∠ABC的角平分线AE、BE相交于点E，延长AE交圆于点D，连接BD、DC，且∠BCA=60°．
（1）求证：△BED为等边三角形；
（2）若∠ADC=30°，⊙O的半径为2
，求BD长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于点E，点F是AC上的动点，BD=DF
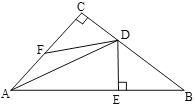
（1）求证：BE=FC；
（2）若∠B=30°，DC=2，此时
，求△ACB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
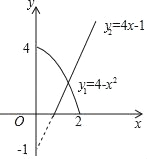
【题目】有一种市场均衡模型是用一次函数和二次函数来刻化的：根据市场调查，某种商品的市场需求量y1（吨）与单价x（百元）之间的关系可看作是二次函数y1=4﹣x2，该商品的市场供应量y2（吨）与单价x（百元）之间的关系可看作是一次函数y2=4x﹣1．
（1）当需求量等于供应量时，市场达到均衡．此时的单价x（百元）称为均衡价格，需求量（供应量）称为均衡数量．求所述市场均衡模型的均衡价格和均衡数量．
（2）当该商品单价为50元时，此时市场供应量与需求量相差多少吨？
（3）根据以上信息分析，当该商品①供不应求②供大于求时，该商品单价分别会在什么范围内？
查看答案和解析>>
科目：初中数学 来源： 题型：
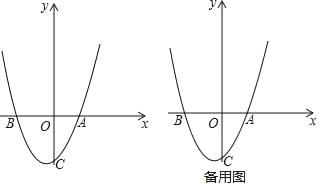
【题目】如图，已知抛物线y=ax2+bx+c（a≠0）经过A（3，0），B（﹣5，0），C（0，﹣5）三点，O为坐标原点．
（1）求此抛物线的解析式；
（2）把抛物线y=ax2+bx+c（a≠0）向上平移
个单位长度，再向左平移n（n＞0）个单位长度得到新抛物线，若新抛物线的顶点M在△ABC内，求n的取值范围；
（3）设点P在y轴上，且满足∠OPA+∠OCA=∠CBA，求CP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知BC是⊙O的直径，点D是BC延长线上一点，AB=AD，AE是⊙O的弦，∠AEC=30°．
（1）求证：直线AD是⊙O的切线；
（2）若AE⊥BC，垂足为M，⊙O的半径为4，求AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
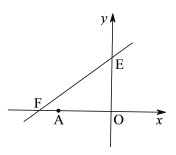
【题目】如图，直线
与x轴、y轴分别相交于点F，E，点A的坐标为(－6，0)，P(x，y)是直线上的一个动点．
（1）试写出点P在运动过程中，△OAP的面积S与x的函数关系式；
（2）当点P运动到什么位置，△OAP的面积为
，求出此时点P的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com