
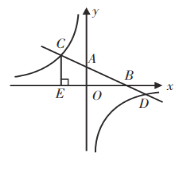
【题目】已知:如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() ,
,![]() 轴交于点
轴交于点![]() ,
,![]() ,与反比例函数的图象分别交于点
,与反比例函数的图象分别交于点![]() ,
,![]() ,
, ![]() 轴于点
轴于点![]() ,
, ![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)求反比例函数的解析式;
(3)连接![]() ,求
,求![]() .
.
【答案】(1)BC=6![]() ;(2)
;(2)![]() ;(3)tan∠BED=
;(3)tan∠BED=![]() .
.
【解析】
(1)根据锐角三角函数![]() ,求出CE,再用勾股定理求出BC的长.
,求出CE,再用勾股定理求出BC的长.
(2)根据已知条件求出C点坐标,用待定系数法求出反比例的函数解析式.
(3)根据![]() . 得
. 得![]() ,即点
,即点![]() 坐标,求出直线与双曲线的交点D的坐标,
坐标,求出直线与双曲线的交点D的坐标,
过D作DF![]() 轴于点F,从而求得答案.
轴于点F,从而求得答案.
(1)![]() ,
,![]()
![]() 轴于点
轴于点![]()
![]()
![]() BC=
BC=![]() =6
=6![]()
(2)由(1)得点![]() 的坐标为
的坐标为![]()
设反比例函数的解析式为![]()
将点![]() 的坐标代入,得
的坐标代入,得![]() ,
,
∴该反比例函数的解析式为y=-![]()
(3)在Rt![]() ABO中,
ABO中, ![]() . 得
. 得![]()
即点![]() 坐标为
坐标为![]()
设直线AC的解析式为y=kx+b.
将A(0,4),B(8,0)代入解析式得
![]()
解得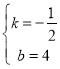
∴直线![]() 的解析式为y=-
的解析式为y=-![]() x+4
x+4
联立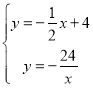 得点
得点![]() 坐标为
坐标为![]()
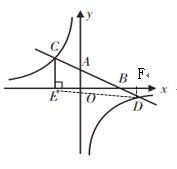
则EF=OF+OE=16,DF=2
连接DE,过D点作DF![]() 轴于点F,
轴于点F,
在Rt![]() DEF中,
DEF中,![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
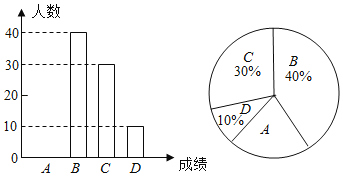
【题目】我校为了了解九年级学生身体素质测试情况,随机抽取了本校九年级部分学生的身体素质测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如图不完整的统计图,请你结合图表所给信息解答下列问题:
(1)请在答题卡上直接将条形统计图补充完整;
(2)扇形统计图中“B”部分所对应的圆心角的度数是 °;
(3)若我校九年级共有1500名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
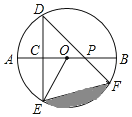
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段公路施工,甲工程队单独施工完成的天数是乙工程队单独施工完天数的2倍,由甲、乙两工程队合作20天可完成,.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)若此项过程由甲工程队单独施工,再由甲、乙两工程队合作施工完成剩下的工程,已知甲工程队每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,要使施工费用不超过64万元,则甲工程队至少要单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
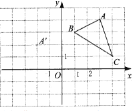
【题目】在平面直角坐标系中,![]() 的三个 顶点的位置如图所示, 点
的三个 顶点的位置如图所示, 点![]() ,现 将
,现 将![]() 平移。使点
平移。使点![]() 变换为点
变换为点![]() ,点
,点![]() 分 别是
分 别是![]() 的对应点.
的对应点.
(1)请画出平移后的图像![]() (不写画法) ,并直接写出点
(不写画法) ,并直接写出点![]() 的坐标:
的坐标: ![]() ;
;
(2)若![]() 内部一点
内部一点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的对应点
的对应点![]() 的坐标是( ).
的坐标是( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
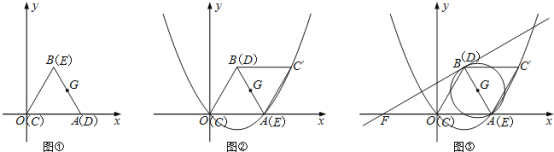
【题目】如图①②,在平面直角坐标系中,边长为2的等边![]() 恰好与坐标系中的
恰好与坐标系中的![]() 重合,现将
重合,现将![]() 绕边
绕边![]() 的中点
的中点![]() 点也是
点也是![]() 的中点),按顺时针方向旋转
的中点),按顺时针方向旋转![]() 到△
到△![]() 的位置.
的位置.
(1)求![]() 点的坐标;
点的坐标;
(2)求经过三点![]() 、
、![]() 、
、![]() 的抛物线的解析式;
的抛物线的解析式;
(3)如图③,![]() 是以
是以![]() 为直径的圆,过
为直径的圆,过![]() 点作
点作![]() 的切线与
的切线与![]() 轴相交于点
轴相交于点![]() ,求切线
,求切线![]() 的解析式;
的解析式;
(4)抛物线上是否存在一点![]() ,使得
,使得![]() .若存在,请求出点
.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,则图中阴影部分的面积为( )
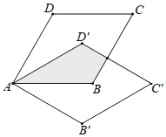
A.1+![]() B.2+
B.2+![]()
C.3D.3–![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为80元,用180元购进甲种玩具的件数与用300元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共32件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1350元,求商场共有几种进货方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com