
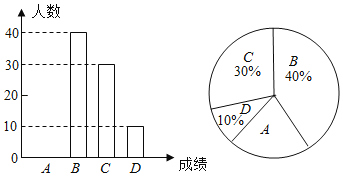
����Ŀ����УΪ���˽���꼶ѧ���������ʲ�������������ȡ�˱�У���꼶����ѧ�����������ʲ��Գɼ�Ϊ��������A�����㣩��B�����ã���C���ϸ�D�����ϸ��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ�����Ƴ���ͼ��������ͳ��ͼ��������ͼ��������Ϣ����������⣺
��1�����ڴ����ֱ�ӽ�����ͳ��ͼ����������
��2������ͳ��ͼ�С�B����������Ӧ��Բ�ĽǵĶ������� ���㣻
��3������У���꼶����1500��ѧ���μ����������ʲ��ԣ��Թ��Ʋ��Գɼ��ϸ����ϣ����ϸ�������
���𰸡���1��100��ͼ�����������2��144����3��1350
��������
��1�����ȸ�������ͳ��ͼ�е�B������������ռ�İٷ��������������Ȼ�����A�����������Ӷ���ȫͳ��ͼ��
��2������B����ռ�İٷֱȳ���360�����������Բ�ĽǵĶ�����
��3�������������Ժϸ�İٷ��ʼ�����ĺϸ��������
�⣺��1��A��ռ�İٷֱ���1��40%��30%��10%��20%��
��ȡ���������ǣ�![]() ��100���ˣ���
��100���ˣ���
A��������100��20%��20���ˣ�����ͼ���£�
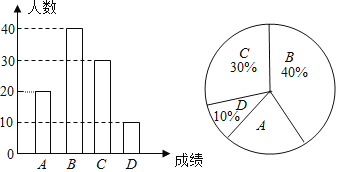
��2������ͳ��ͼ����B����������Ӧ��Բ�ĽǵĶ�����360���40%��144����
�ʴ�Ϊ��144��
��3����������ã�
1500����1��10%����1350���ˣ���
�𣺲��Գɼ��ϸ����ϣ����ϸ�����Ϊ1350�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ���ı��εĶԽ��߰��ı��ηֳ����������Σ�һ���ǵȱ������Σ���һ���ǸöԽ������ԵĽ�Ϊ![]() �������Σ����ǰ������Խ��߽�������ı��ε�����Խ��ߣ�����ı��γ�Ϊ�����ı��Σ�
�������Σ����ǰ������Խ��߽�������ı��ε�����Խ��ߣ�����ı��γ�Ϊ�����ı��Σ�
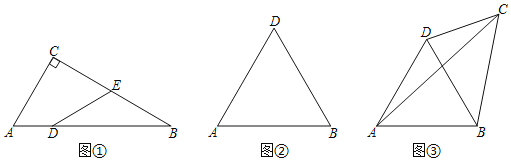
��1����ͼ������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ��һ�㣬
��һ�㣬![]() ��
��![]() Ϊ
Ϊ![]() �е㣬����
�е㣬����![]() ����֤���ı���
����֤���ı���![]() Ϊ�����ı��Σ�
Ϊ�����ı��Σ�
��2����ͼ����![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() Ϊ����Խ��ߣ��ı���
Ϊ����Խ��ߣ��ı���![]() Ϊ�����ı��Σ��뻭ͼ�ҳ�����������C������������ͼ���ϣ�(��ͼ�б����Ҫ������)
Ϊ�����ı��Σ��뻭ͼ�ҳ�����������C������������ͼ���ϣ�(��ͼ�б����Ҫ������)
��3���ڣ�2���������£�
����![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�![]() ����
����![]() �ij��ȣ�
�ij��ȣ�
����ͼ������![]() ��
��![]() ��
��![]() ����ֱ��д��
����ֱ��д��![]() ��
��![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,���߳�Ϊ12��������ABCD����Խ���AC����,�ٰѡ�ABC����AD����ƽ��,�õ���A��B��C��,�������������ص����ֵ����Ϊ32ʱ,���ƶ��ľ���AA�����________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
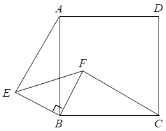
����Ŀ����ͼ����EBFΪ����ֱ�������Σ���BΪֱ�Ƕ��㣬 �ı���ABCD�������Σ�
�� ��֤����ABE�ա�CBF��
�� CF��AE��ʲô�����λ�ù�ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
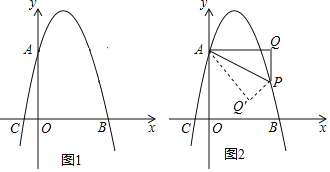
����Ŀ����ͼ1����֪������y����x2+bx+c��y���ڵ�A(0��4)����x���ڵ�B(4��0)����P����������һ���㣬�Թ���P��x��Ĵ���1���ٹ���A��1�Ĵ��ߣ�����ΪQ������AP��
(1)�������ߵĺ�������ʽ�͵�C�����ꣻ
(2)����AQP�ס�AOC�����P�ĺ����ꣻ
(3)��ͼ2������Pλ�������ߵĶԳ�����Ҳ�ʱ��������APQ��AP���ۣ���Q�Ķ�Ӧ��Ϊ��Q�䣬��ֱ��д������Q��������������ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˼ά̽����
��������ABCD�У�AB��4����EAF�����߷ֱ�����CB��DC�ڵ�E��F����EAF��45�㣮
��1����ͼ1������E��F�ֱ����߶�BC��CD��ʱ����CEF���ܳ����� ����
��2����ͼ2������E��F�ֱ���CB��DC���ӳ����ϣ�CF��2ʱ�����CEF���ܳ���
��չ������
��ͼ3����Rt��ABC�У���ACB��90�㣬CA��CB������B��BD��BC������AD����BC���ӳ�����ȡһ��E��ʹ��EDA��30�㣬����AE����BD��2����EAD��45��ʱ����ֱ��д���߶�CE�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��E�Ǿ���ABCD�ı�BC��һ�㣬EF��AE���ֱ�AC��CD�ڵ�M��F��BG��AC������ΪG��BG��AE�ڵ�H��
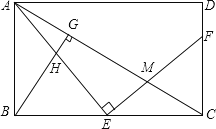
��1����֤����ABE�ס�ECF��
��2���ҳ����ABH���Ƶ������Σ���֤����
��3����E��BC�е㣬BC=2AB��AB=4����EM�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD�У���E�DZ�BC��һ�㣬����AE������E��EM��AE�����Խ���AC�ڵ�M������M��MN��AB������ΪN������NE��


��1����֤��AE=![]() NE+ME��
NE+ME��
��2����ͼ2���ӳ�EM����F��ʹEF=EA������AF������F��FH��DC������ΪH������CH��FH���ڵ�������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
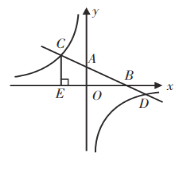
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �ֱ���
�ֱ���![]() ,
,![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ���뷴����������ͼ��ֱ��ڵ�
���뷴����������ͼ��ֱ��ڵ�![]() ��
��![]() ��
�� ![]() ���ڵ�
���ڵ�![]() ��
�� ![]() ,
,![]() ��
��![]() .
.
��1����![]() �ij���
�ij���
��2�����������Ľ���ʽ��
��3������![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com