
ΓΨΧβΡΩΓΩ»γΙϊ“ΜΗωΥΡ±Ώ–ΈΒΡΕ‘Ϋ«œΏΑ―ΥΡ±Ώ–ΈΖ÷≥…ΝΫΗω»ΐΫ«–ΈΘ§“ΜΗω «Β»±Ώ»ΐΫ«–ΈΘ§Νμ“ΜΗω «ΗΟΕ‘Ϋ«œΏΥυΕ‘ΒΡΫ«ΈΣ![]() ΒΡ»ΐΫ«–ΈΘ§Έ“Ο«Α―’βΧθΕ‘Ϋ«œΏΫ–Ήω’βΗωΥΡ±Ώ–ΈΒΡάμœκΕ‘Ϋ«œΏΘ§’βΗωΥΡ±Ώ–Έ≥ΤΈΣάμœκΥΡ±Ώ–ΈΘ°
ΒΡ»ΐΫ«–ΈΘ§Έ“Ο«Α―’βΧθΕ‘Ϋ«œΏΫ–Ήω’βΗωΥΡ±Ώ–ΈΒΡάμœκΕ‘Ϋ«œΏΘ§’βΗωΥΡ±Ώ–Έ≥ΤΈΣάμœκΥΡ±Ώ–ΈΘ°
Θ®1Θ©»γΆΦΔΌΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() …œ“ΜΒψΘ§
…œ“ΜΒψΘ§![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ÷–ΒψΘ§Ν§Ϋ”
÷–ΒψΘ§Ν§Ϋ”![]() Θ§«σ÷ΛΘΚΥΡ±Ώ–Έ
Θ§«σ÷ΛΘΚΥΡ±Ώ–Έ![]() ΈΣάμœκΥΡ±Ώ–ΈΘΜ
ΈΣάμœκΥΡ±Ώ–ΈΘΜ
Θ®2Θ©»γΆΦΔΎΘ§![]() «Β»±Ώ»ΐΫ«–ΈΘ§»τ
«Β»±Ώ»ΐΫ«–ΈΘ§»τ![]() ΈΣάμœκΕ‘Ϋ«œΏΘ§ΥΡ±Ώ–Έ
ΈΣάμœκΕ‘Ϋ«œΏΘ§ΥΡ±Ώ–Έ![]() ΈΣάμœκΥΡ±Ώ–ΈΘ°«κΜ≠ΆΦ’“≥ωΖϊΚœΧθΦΰΒΡCΒψ¬δ‘Ύ‘θ―υΒΡΆΦ–Έ…œΘΜ(‘ΎΆΦ÷–±ξ≥ω±Ί“ΣΒΡ ΐΨί)
ΈΣάμœκΥΡ±Ώ–ΈΘ°«κΜ≠ΆΦ’“≥ωΖϊΚœΧθΦΰΒΡCΒψ¬δ‘Ύ‘θ―υΒΡΆΦ–Έ…œΘΜ(‘ΎΆΦ÷–±ξ≥ω±Ί“ΣΒΡ ΐΨί)
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§
ΔΌ»τ![]() ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§
ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§![]() Θ§«σ
Θ§«σ![]() ΒΡ≥ΛΕ»ΘΜ
ΒΡ≥ΛΕ»ΘΜ
ΔΎ»γΆΦΔέΘ§»τ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§«κ÷±Ϋ”–¥≥ω
Θ§«κ÷±Ϋ”–¥≥ω![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ°
÷°ΦδΒΡ ΐΝΩΙΊœΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©œξΦϊΫβΈωΘΜΘ®2Θ©œξΦϊΫβΈωΘΜΘ®3Θ©ΔΌ![]() Μρ
Μρ![]() ΘΜ ΔΎ
ΘΜ ΔΎ![]()
ΓΨΫβΈωΓΩ
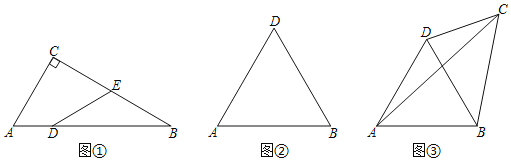
Θ®1Θ©Ν§Ϋ”CDΘ§ΙΐΒψEΉςEMΓΆABΘ§“Ή÷ΛEM «BDΒΡ÷–¥ΙœΏΘ§ΒΟΓœEDB=ΓœB=30ΓψΘ§¥”ΕχΒΟΓœCED=60ΓψΘ§ΫχΕχΒΟ![]() «Β»±Ώ»ΐΫ«–ΈΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
«Β»±Ώ»ΐΫ«–ΈΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®2Θ©ΉςΒ»―ϋ»ΐΫ«–ΈODBΘ§ ΙΒΟODΘΫOBΘ§ΓœDOBΘΫ120ΓψΘ§“‘OΈΣ‘≤–ΡΘ§ODΈΣΑκΨΕΉςΓ―OΘ§Β±ΒψC‘ΎΜΓBCD…œ ±Θ§¬ζΉψΧθΦΰΘΜ
Θ®3Θ©ΔΌ»τ![]() ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘΚΘ®iΘ©Β±ΓœBDC=90Γψ ±ΘΜΘ®iiΘ©Β±ΓœDBC=90Γψ ±Θ§Ζ÷±π«σ≥ω¥πΑΗΦ¥Ω…ΘΜΔΎΫΪ
ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘΚΘ®iΘ©Β±ΓœBDC=90Γψ ±ΘΜΘ®iiΘ©Β±ΓœDBC=90Γψ ±Θ§Ζ÷±π«σ≥ω¥πΑΗΦ¥Ω…ΘΜΔΎΫΪ![]() »ΤΒψDΡφ ±’κ–ΐΉΣ60ΓψΘ§ΒΟΒΫ
»ΤΒψDΡφ ±’κ–ΐΉΣ60ΓψΘ§ΒΟΒΫ![]() Θ§Ν§Ϋ”ECΘ§ΙΐΒψEΉςEFΓΆBCΘ§ΫΜBCΒΡ―”≥ΛœΏ”ΎΒψFΘ§Ω…ΒΟ
Θ§Ν§Ϋ”ECΘ§ΙΐΒψEΉςEFΓΆBCΘ§ΫΜBCΒΡ―”≥ΛœΏ”ΎΒψFΘ§Ω…ΒΟ![]() «Β»±Ώ»ΐΫ«–ΈΘ§”ΟΚ§xΘ§yΒΡ¥ζ ΐ Ϋ±μ ΨEFΘ§CFΘ§ΫχΕχΒΟΒΫBFΒΡ±μ¥ο ΫΘ§άϊ”ΟΙ¥Ι…Ε®άμΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘ°
«Β»±Ώ»ΐΫ«–ΈΘ§”ΟΚ§xΘ§yΒΡ¥ζ ΐ Ϋ±μ ΨEFΘ§CFΘ§ΫχΕχΒΟΒΫBFΒΡ±μ¥ο ΫΘ§άϊ”ΟΙ¥Ι…Ε®άμΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘ°
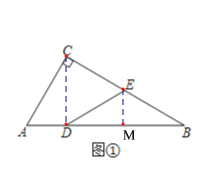
Θ®1Θ©Ν§Ϋ”CDΘ§ΙΐΒψEΉςEMΓΆABΘ§»γΆΦΔΌΘ§
ΓΏ‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
ΓύAB=4Θ§BC=![]() Θ§BD=4-1=3Θ§
Θ§BD=4-1=3Θ§
ΓΏ![]() ΈΣ
ΈΣ![]() ÷–ΒψΘ§
÷–ΒψΘ§
ΓύBE=![]() Θ§
Θ§
ΓΏ‘Ύ![]() ÷–Θ§ΓœB=30ΓψΘ§EMΓΆABΘ§
÷–Θ§ΓœB=30ΓψΘ§EMΓΆABΘ§
ΓύBM=BEcos30Γψ=![]() Θ§
Θ§
ΓύDM=BM=![]() Θ§Φ¥EM «BDΒΡ÷–¥ΙœΏΘ§
Θ§Φ¥EM «BDΒΡ÷–¥ΙœΏΘ§
ΓύED=EB=ECΘ§
ΓύΓœEDB=ΓœB=30ΓψΘ§
ΓύΓœCED=60ΓψΘ§
Γύ![]() «Β»±Ώ»ΐΫ«–ΈΘ§
«Β»±Ώ»ΐΫ«–ΈΘ§
”÷ΓΏΓœA=180Γψ-ΓœB-ΓœACB=60ΓψΘ§
ΓύΥΡ±Ώ–Έ![]() ΈΣάμœκΥΡ±Ώ–ΈΘΜ
ΈΣάμœκΥΡ±Ώ–ΈΘΜ
Θ®2Θ©»γΆΦΔΎ÷–Θ§ΉςΒ»―ϋ»ΐΫ«–ΈODBΘ§ ΙΒΟODΘΫOBΘ§ΓœDOBΘΫ120ΓψΘ§“‘OΈΣ‘≤–ΡΘ§ODΈΣΑκΨΕΉςΓ―OΘ§Β±ΒψC‘ΎΜΓBCD…œ ±Θ§ΓœDCBΘΫ![]() ΓœDOBΘΫ60ΓψΘ§¬ζΉψΧθΦΰΘΜ
ΓœDOBΘΫ60ΓψΘ§¬ζΉψΧθΦΰΘΜ
Θ®3Θ©ΔΌ»τ![]() ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘΚ
ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘΚ
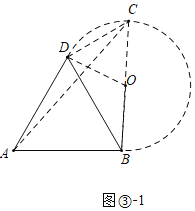
Θ®iΘ©Β±ΓœBDC=90Γψ ±Θ§»γΆΦΔέ-1Θ§
ΓΏΓœBCD=60ΓψΘ§BC=2Θ§
ΓύΓœDBC=30ΓψΘ§BD=BC![]() cos30Γψ=
cos30Γψ=![]() Θ§
Θ§
ΓΏ![]() «Β»±Ώ»ΐΫ«–ΈΘ§
«Β»±Ώ»ΐΫ«–ΈΘ§
ΓύAB=BD=![]() Θ§ΓœABD=60ΓψΘ§
Θ§ΓœABD=60ΓψΘ§
ΓύΓœABC=90ΓψΘ§
Γύ![]() ΘΜ
ΘΜ
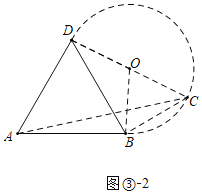
Θ®iiΘ©Β±ΓœDBC=90Γψ ±Θ§»γΆΦΔέ-2Θ§
Ά§άμΩ…ΒΟΘΚΓœADC=90ΓψΘ§DC=4Θ§AD=![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
Ήέ…œΥυ ωΘΚAC=![]() Μρ
Μρ![]() ΘΜ
ΘΜ
ΔΎΫΪ![]() »ΤΒψDΡφ ±’κ–ΐΉΣ60ΓψΘ§ΒΟΒΫ
»ΤΒψDΡφ ±’κ–ΐΉΣ60ΓψΘ§ΒΟΒΫ![]() Θ§Ν§Ϋ”ECΘ§ΙΐΒψEΉςEFΓΆBCΘ§ΫΜBCΒΡ―”≥ΛœΏ”ΎΒψFΘ§»γΆΦΔήΘ§
Θ§Ν§Ϋ”ECΘ§ΙΐΒψEΉςEFΓΆBCΘ§ΫΜBCΒΡ―”≥ΛœΏ”ΎΒψFΘ§»γΆΦΔήΘ§
ΓύΓœCDE=60ΓψΘ§ED=CDΘ§BE=AC=zΘ§
Γύ![]() «Β»±Ώ»ΐΫ«–ΈΘ§
«Β»±Ώ»ΐΫ«–ΈΘ§
ΓύEC=CD=xΘ§ΓœDCE=60ΓψΘ§
ΓΏΓœBCD=60ΓψΘ§
ΓύΓœECF=180Γψ-60Γψ-60Γψ=60ΓψΘ§
ΓύEF=EC![]() sin60Γψ=
sin60Γψ=![]() Θ§CF= EC
Θ§CF= EC![]() cos60Γψ=
cos60Γψ=![]() Θ§
Θ§
ΓύBF=BC+CF=y+![]() Θ§
Θ§
ΓύBE=![]() =
=![]() Θ§
Θ§
Γύz=![]() Θ§Φ¥ΘΚ
Θ§Φ¥ΘΚ![]() Θ°
Θ°




| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
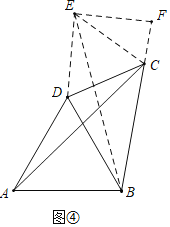
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏABΨ≠ΙΐΓ―O…œΒΡΒψCΘ§≤Δ«“OAΘΫOBΘ§CAΘΫCBΘ§Γ―OΫΜ÷±œΏOB”ΎEΘ§DΘ§Ν§Ϋ”ECΘ§CDΘ°
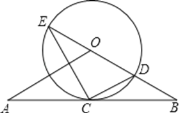
Θ®1Θ©«σ÷ΛΘΚ÷±œΏAB «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ© ‘≤¬œκBCΘ§BDΘ§BE»ΐ’Ώ÷°ΦδΒΡΒ»ΝΩΙΊœΒΘ§≤ΔΦ”“‘÷ΛΟςΘΜ
Θ®3Θ©»τtanΓœCEDΘΫ![]() Θ§Γ―OΒΡΑκΨΕΈΣ3Θ§«σOAΒΡ≥ΛΘ°
Θ§Γ―OΒΡΑκΨΕΈΣ3Θ§«σOAΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
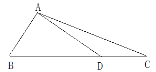
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ÷±Ϋ«ΓςBAD÷–―”≥Λ–±±ΏBDΒΫΒψCΘ§ Ι![]() Θ§»τ
Θ§»τ![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡ÷ΒΈΣΘ® Θ©
ΒΡ÷ΒΈΣΘ® Θ©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
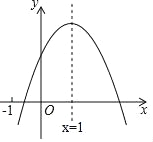
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐyΘΫax2+bx+cΘ®aΓΌ0Θ©ΒΡΆΦœσ”κx÷αΫΜ”ΎΘ®x1Θ§0Θ©Θ§«“©¹1ΘΦx1ΘΦ0Θ§Ε‘≥Τ÷αxΘΫ1Θ°»γΆΦΥυ ΨΘ§”–œ¬Ν–5ΗωΫα¬έΘΚΔΌabcΘΨ0ΘΜΔΎbΘΦa+cΘΜΔέ4a+2b+cΘΨ0ΘΜΔή2cΘΦ3bΘΜΔίa+bΘΨmΘ®am+bΘ©Θ®mΓΌ1ΒΡ Β ΐΘ©Θ°Τδ÷–Υυ”–Ϋα¬έ’ΐ»ΖΒΡ «______Θ®Χν–¥Ζ§Κ≈Θ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβΡ≥–Θ―ß…ζΕ‘ΓΕΉν«Ω¥σΡ‘ΓΖΓΔΓΕά ΕΝ’ΏΓΖΓΔΓΕ÷–Ιζ Ϊ¥ ¥σΜαΓΖΓΔΓΕ≥ω≤ ÷–Ιζ»ΥΓΖΥΡΗωΒγ ”ΫΎΡΩΒΡœ≤Α°«ιΩωΘ§Υφ•i≥ι»ΓΝΥ![]() Οϊ―ß…ζΫχ––Βς≤ιΆ≥ΦΤΘ®“Σ«σΟΩΟϊ―ß…ζ―Γ≥ω≤Δ«“÷ΜΡή―Γ≥ω“ΜΗωΉ‘ΦΚΉνœ≤Α°ΒΡΫΎΡΩΘ©Θ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…»γΆΦΆ≥ΦΤΆΦ±μΘΚ
Οϊ―ß…ζΫχ––Βς≤ιΆ≥ΦΤΘ®“Σ«σΟΩΟϊ―ß…ζ―Γ≥ω≤Δ«“÷ΜΡή―Γ≥ω“ΜΗωΉ‘ΦΚΉνœ≤Α°ΒΡΫΎΡΩΘ©Θ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…»γΆΦΆ≥ΦΤΆΦ±μΘΚ
―ß…ζΉνœ≤Α°ΒΡΫΎΡΩ»Υ ΐΆ≥ΦΤ±μ
ΫΎΡΩ | »Υ ΐΘ®ΟϊΘ© | ΑΌΖ÷±» |
Ήν«Ω¥σΡ‘ | 5 | 10% |
ά ΕΝ’Ώ | 15 | |
÷–Ιζ Ϊ¥ ¥σΜα |
| 40% |
≥ω≤ ÷–Ιζ»Υ | 10 | 20% |
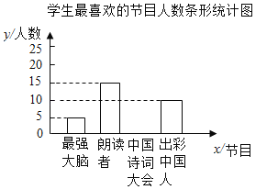
ΗυΨί“‘…œ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©![]() ΓΓΘ§
ΓΓΘ§![]() ΓΓΘΜ
ΓΓΘΜ
Θ®2Θ©≤Ι»Ϊ…œΟφΒΡΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®3Θ©»τΗΟ–ΘΙ≤”–―ß…ζ![]() ΟϊΘ§ΙάΦΤΗΟ–Θ―ß…ζΉνœ≤Α°ΓΕά ΕΝ’ΏΓΖΫΎΡΩΒΡ»Υ ΐΘ°
ΟϊΘ§ΙάΦΤΗΟ–Θ―ß…ζΉνœ≤Α°ΓΕά ΕΝ’ΏΓΖΫΎΡΩΒΡ»Υ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝ“‘œ¬≤ΡΝœΘΚΕ‘ ΐΒΡ¥¥ Φ»Υ «Υ’ΗώάΦ ΐ―ßΦ“Ρ…ΤΛΕϊΘ®JΘ°NapierΘ§1550Ρξ-1617ΡξΘ©Θ§Ρ…ΤΛΕϊΖΔΟςΕ‘ ΐ «‘Ύ÷Η ΐΗ≈ΡνΫ®ΝΔ÷°«ΑΘ§÷±ΒΫ18 άΦΆ»π Ω ΐ―ßΦ“≈Ζά≠Θ®EulerΘ§1707Ρξ-1783ΡξΘ©≤≈ΖΔœ÷÷Η ΐ”κΕ‘ ΐ÷°ΦδΒΡΝΣœΒΘ°Ε‘ ΐΒΡΕ®“εΘΚ“ΜΑψΒΊΘ§»τ![]() Θ§‘ρ
Θ§‘ρ![]() Ϋ–Ήω“‘
Ϋ–Ήω“‘![]() ΈΣΒΉ
ΈΣΒΉ![]() ΒΡΕ‘ ΐΘ§Φ«Ής
ΒΡΕ‘ ΐΘ§Φ«Ής![]() Θ°±»»γ÷Η ΐ Ϋ
Θ°±»»γ÷Η ΐ Ϋ![]() Ω…“‘ΉΣΜ·ΈΣ
Ω…“‘ΉΣΜ·ΈΣ![]() Θ§Ε‘ ΐ Ϋ
Θ§Ε‘ ΐ Ϋ![]() Ω…“‘ΉΣΜ·ΈΣ
Ω…“‘ΉΣΜ·ΈΣ![]() Θ°Έ“Ο«ΗυΨίΕ‘ ΐΒΡΕ®“εΩ…ΒΟΒΫΕ‘ ΐΒΡ“ΜΗω–‘÷ ΘΚ
Θ°Έ“Ο«ΗυΨίΕ‘ ΐΒΡΕ®“εΩ…ΒΟΒΫΕ‘ ΐΒΡ“ΜΗω–‘÷ ΘΚ![]()
![]() Θ°άμ”…»γœ¬ΘΚ…η
Θ°άμ”…»γœ¬ΘΚ…η![]() Θ§
Θ§![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§
Θ§![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§”…Ε‘ ΐΒΡΕ®“εΒΟ
Θ§”…Ε‘ ΐΒΡΕ®“εΒΟ![]() Θ§”÷“ρΈΣ
Θ§”÷“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ°ΫβΨω“‘œ¬Έ ΧβΘΚ
Θ°ΫβΨω“‘œ¬Έ ΧβΘΚ
Θ®1Θ©ΫΪ÷Η ΐ![]() ΉΣΜ·ΈΣΕ‘ ΐ ΫΘΚ Θ°
ΉΣΜ·ΈΣΕ‘ ΐ ΫΘΚ Θ°
Θ®2Θ©Ζ¬’’…œΟφΒΡ≤ΡΝœΘ§ ‘÷ΛΟςΘΚ![]()
Θ®3Θ©ΆΊ’Ι‘Υ”ΟΘΚΦΤΥψ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–¬ΫΜΆ®Ζ®Ιφ Β ©“‘ά¥Θ§ΈΣΝΥΫβΡ≥…γ«χΨ”ΟώΉώ ΊΫΜΆ®Ζ®Ιφ«ιΩωΘ§–ΓΟςΥφΜζ―Γ»Γ≤ΩΖ÷Ψ”ΟώΨΆΓΑ––»Υ¥≥ΚλΒΤœ÷œσΓ±Ϋχ––Έ ΨμΒς≤ιΘ§Βς≤ιΖ÷ΈΣΓΑAΘΚ¥”≤Μ¥≥ΚλΒΤΘΜBΘΚ≈ΦΕϊ¥≥ΚλΒΤΘΜCΘΚΨ≠≥Θ¥≥ΚλΒΤΘΜDΘΚΤδΥϊΓ±ΥΡ÷÷«ιΩωΘ§≤ΔΗυΨίΒς≤ιΫαΙϊΜφ÷Τ≥ω≤ΩΖ÷Χθ–ΈΆ≥ΦΤΆΦΘ®»γΆΦ1Θ©ΚΆ≤ΩΖ÷…»–ΈΆ≥ΦΤΆΦΘ®»γΆΦ2Θ©Θ°«κΗυΨίΆΦ÷––≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
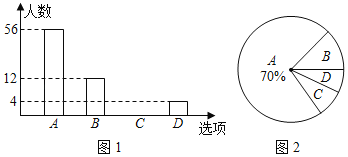
Θ®1Θ©±Ψ¥ΈΒς≤ιΙ≤―Γ»ΓΓΓ ΓΓΟϊΨ”ΟώΘΜ
Θ®2Θ©«σ≥ω…»–ΈΆ≥ΦΤΆΦ÷–ΓΑCΓ±ΥυΕ‘…»–ΈΒΡ‘≤–ΡΫ« «ΓΓ ΓΓΕ»Θ§≤ΔΫΪΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©»γΙϊΗΟ…γ«χΙ≤”–Ψ”Οώ2600»ΥΘ§ΙάΦΤ”–Εύ…Ό»Υ¥”≤Μ¥≥ΚλΒΤΘΩΘ®«κΦΤΥψΥΒΟςΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
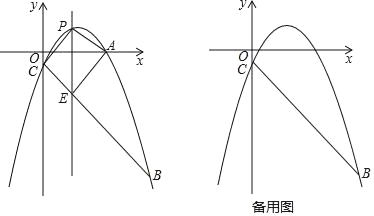
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏy=©¹![]() x2+bx+cΨ≠ΙΐΒψAΘ®5Θ§
x2+bx+cΨ≠ΙΐΒψAΘ®5Θ§![]() Θ©ΓΔΒψBΘ®9Θ§©¹10Θ©Θ§”κy÷αΫΜ”ΎΒψCΘ§ΒψP «÷±œΏAC…œΖΫ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘΜ
Θ©ΓΔΒψBΘ®9Θ§©¹10Θ©Θ§”κy÷αΫΜ”ΎΒψCΘ§ΒψP «÷±œΏAC…œΖΫ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘΜ
Θ®1Θ©«σ≈ΉΈοœΏΕ‘”ΠΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©ΙΐΒψP«“”κy÷αΤΫ––ΒΡ÷±œΏl”κ÷±œΏBCΫΜ”ΎΒψEΘ§Β±ΥΡ±Ώ–ΈAECPΒΡΟφΜΐΉν¥σ ±Θ§«σΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©Β±ΓœPCB=90Γψ ±Θ§ΉςΓœPCBΒΡΫ«ΤΫΖ÷œΏΘ§ΫΜ≈ΉΈοœΏ”ΎΒψFΘ°
ΔΌ«σΒψPΚΆΒψFΒΡΉχ±ξΘΜ
ΔΎ‘Ύ÷±œΏCF…œ «Ζώ¥φ‘ΎΒψQΘ§ ΙΒΟ“‘FΓΔPΓΔQΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςBCFœύΥΤΘ§»τ¥φ‘ΎΘ§«σ≥ωΒψQΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
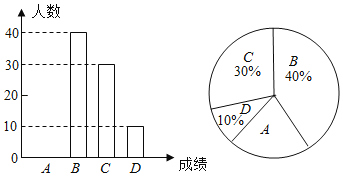
ΓΨΧβΡΩΓΩΈ“–ΘΈΣΝΥΝΥΫβΨ≈ΡξΦΕ―ß…ζ…μΧεΥΊ÷ ≤β ‘«ιΩωΘ§ΥφΜζ≥ι»ΓΝΥ±Ψ–ΘΨ≈ΡξΦΕ≤ΩΖ÷―ß…ζΒΡ…μΧεΥΊ÷ ≤β ‘≥…Φ®ΈΣ―υ±ΨΘ§Α¥AΘ®”≈–ψΘ©ΓΔBΘ®ΝΦΚΟΘ©ΓΔCΘ®ΚœΗώΘ©ΓΔDΘ®≤ΜΚœΗώΘ©ΥΡΗωΒ»ΦΕΫχ––Ά≥ΦΤΘ§≤ΔΫΪΆ≥ΦΤΫαΙϊΜφ÷Τ≥…»γΆΦ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΡψΫαΚœΆΦ±μΥυΗχ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©«κ‘Ύ¥πΧβΩ®…œ÷±Ϋ”ΫΪΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®2Θ©…»–ΈΆ≥ΦΤΆΦ÷–ΓΑBΓ±≤ΩΖ÷ΥυΕ‘”ΠΒΡ‘≤–ΡΫ«ΒΡΕ» ΐ «ΓΓ ΓΓΓψΘΜ
Θ®3Θ©»τΈ“–ΘΨ≈ΡξΦΕΙ≤”–1500Οϊ―ß…ζ≤ΈΦ”ΝΥ…μΧεΥΊ÷ ≤β ‘Θ§ ‘ΙάΦΤ≤β ‘≥…Φ®ΚœΗώ“‘…œΘ®Κ§ΚœΗώΘ©ΒΡ»Υ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com