
【题目】阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550年-1617年),纳皮尔发明对数是在指数概念建立之前,直到18世纪瑞士数学家欧拉(Euler,1707年-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若![]() ,则
,则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() .比如指数式
.比如指数式![]() 可以转化为
可以转化为![]() ,对数式
,对数式![]() 可以转化为
可以转化为![]() .我们根据对数的定义可得到对数的一个性质:
.我们根据对数的定义可得到对数的一个性质:![]()
![]() .理由如下:设
.理由如下:设![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,由对数的定义得
,由对数的定义得![]() ,又因为
,又因为![]() ,所以
,所以![]() .解决以下问题:
.解决以下问题:
(1)将指数![]() 转化为对数式: .
转化为对数式: .
(2)仿照上面的材料,试证明:![]()
(3)拓展运用:计算![]() .
.
【答案】(1)![]() ;(2)见解析;(3)2
;(2)见解析;(3)2
【解析】
(1)根据题意可以把指数式53=125写成对数式;
(2)先设logaM=x,logaN=y,根据对数的定义可表示为指数式为:M=ax,N=ay,计算![]() 的结果,同理由所给材料的证明过程可得结论;
的结果,同理由所给材料的证明过程可得结论;
(3)根据公式:loga(MN)=logaM+logaN和![]() 的逆用,将所求式子表示为:log3(2×18÷4),计算可得结论.
的逆用,将所求式子表示为:log3(2×18÷4),计算可得结论.
(1)∵一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:记作:x=logaN.
∴3=log5125,
故答案为:3=log5125;
(2)证明:设![]() ,
,![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
由对数的定义得![]()
又∵![]() ,
,
∴![]()
(3)![]() log3(2×18÷4)= log39=2.
log3(2×18÷4)= log39=2.
故答案为:2.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案科目:初中数学 来源: 题型:
【题目】某文具店每天售出甲、乙两种笔,统计后发现:甲、乙两种笔同一天售出量之间满足一次函数的关系,设甲、乙两种笔同一天的售出量分别为x(支)、y(支),部分数据如表所示(下表中每一列数据表示甲、乙两种笔同一天的售出量).
甲种笔售出x(支) | … | 4 | 6 | 8 | … |
乙种笔售出y(支) | … | 6 | 12 | 18 | … |
(1)求y关于x的函数关系式;(不需要写出函数的定义域)
(2)某一天文具店售出甲、乙两种笔的营业额分别为30元和120元,如果乙种笔每支售价比甲种笔每支售价多2元,那么甲、乙两种笔这天各售出多少支?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3cm、AC=4cm、BC=5cm,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画的条数为( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C,连接BC.
轴交于点C,连接BC.
(1)如图1,求直线BC的表达式;
(2)如图1,点P是抛物线上位于第一象限内的一点,连接PC,PB,当△PCB面积最大时,一动点Q从点P从出发,沿适当路径运动到![]() 轴上的某个点G处,再沿适当路径运动到
轴上的某个点G处,再沿适当路径运动到![]() 轴上的某个点H处,最后到达线段BC的中点F处停止,求当△PCB面积最大时,点P的坐标及点Q在整个运动过程中经过的最短路径的长;
轴上的某个点H处,最后到达线段BC的中点F处停止,求当△PCB面积最大时,点P的坐标及点Q在整个运动过程中经过的最短路径的长;
(3)如图2,在(2)的条件下,当△PCB面积最大时,把抛物线![]() 向右平移使它的图象经过点P,得到新抛物线
向右平移使它的图象经过点P,得到新抛物线![]() ,在新抛物线
,在新抛物线![]() 上,是否存在点E,使△ECB的面积等于△PCB的面积.若存在,请求出点E的坐标,若不存在,请说明理由.
上,是否存在点E,使△ECB的面积等于△PCB的面积.若存在,请求出点E的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个四边形的对角线把四边形分成两个三角形,一个是等边三角形,另一个是该对角线所对的角为![]() 的三角形,我们把这条对角线叫做这个四边形的理想对角线,这个四边形称为理想四边形.
的三角形,我们把这条对角线叫做这个四边形的理想对角线,这个四边形称为理想四边形.
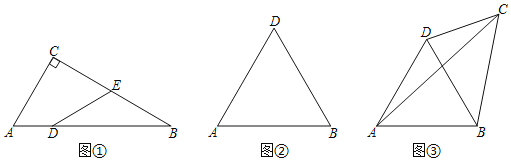
(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,求证:四边形
,求证:四边形![]() 为理想四边形;
为理想四边形;
(2)如图②,![]() 是等边三角形,若
是等边三角形,若![]() 为理想对角线,四边形
为理想对角线,四边形![]() 为理想四边形.请画图找出符合条件的C点落在怎样的图形上;(在图中标出必要的数据)
为理想四边形.请画图找出符合条件的C点落在怎样的图形上;(在图中标出必要的数据)
(3)在(2)的条件下,
①若![]() 为直角三角形,
为直角三角形,![]() ,求
,求![]() 的长度;
的长度;
②如图③,若![]() ,
,![]() ,
,![]() ,请直接写出
,请直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,则下列结论:①b2﹣4ac>0;②ac<0;③m>2,其中正确结论的个数是( )

A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:对数的创始人是苏格兰数学家纳皮尔,纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉才发现指数与对数之间的联系.
对数的定义:一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:记作:x=logaN.比如指数式24=16可以转化为4=log216,对数式2=log525可以转化为52=25.
我们根据对数的定义可得到对数的一个性质:
loga(MN)=logaM+logaN(a>0,a≠1,M>0,N>0);理由如下:logaM=m,logaN=n,则M=am,N=an
∴MN=aman=am+n,由对数的定义得m+n=loga(MN)
又∵m+n=logaM+logaN
∴loga(MN)=logaM+logaN
解决以下问题:
(1)将指数式53=125转化为对数式 ;
(2)log24= ,log381= ,log464= .(直接写出结果)
(3)证明:证明loga![]() =logaM﹣logaN(a>0,a≠1,M>0,N>0).(写出证明过程)
=logaM﹣logaN(a>0,a≠1,M>0,N>0).(写出证明过程)
(4)拓展运用:计算计算log34+log312﹣log316= .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
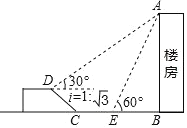
【题目】如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面![]() 处测得楼房顶部
处测得楼房顶部![]() 的仰角为
的仰角为![]() ,沿坡面向下走到坡脚
,沿坡面向下走到坡脚![]() 处,然后向楼房方向继续行走10米到达
处,然后向楼房方向继续行走10米到达![]() 处,测得楼房顶部
处,测得楼房顶部![]() 的仰角为
的仰角为![]() .已知坡面
.已知坡面![]() 米,山坡的坡度
米,山坡的坡度![]() (坡度
(坡度![]() 是指坡面的铅直高度与水平宽度的比),求楼房
是指坡面的铅直高度与水平宽度的比),求楼房![]() 高度.(结果精确到0.1米)(参考数据:
高度.(结果精确到0.1米)(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】思维探索:
在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
(1)如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是 ;
(2)如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;
拓展提升:
如图3,在Rt△ABC中,∠ACB=90°,CA=CB,过点B作BD⊥BC,连接AD,在BC的延长线上取一点E,使∠EDA=30°,连接AE,当BD=2,∠EAD=45°时,请直接写出线段CE的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com