
ЁОЬтФПЁПХзЮяЯп![]() гы
гы![]() жсНЛгкAЃЌBСНЕуЃЌгы
жсНЛгкAЃЌBСНЕуЃЌгы![]() жсНЛгкЕуCЃЌСЌНгBCЃЎ
жсНЛгкЕуCЃЌСЌНгBCЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжБЯпBCЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуPЪЧХзЮяЯпЩЯЮЛгкЕквЛЯѓЯоФкЕФвЛЕуЃЌСЌНгPCЃЌPBЃЌЕБЁїPCBУцЛ§зюДѓЪБЃЌвЛЖЏЕуQДгЕуPДгГіЗЂЃЌбиЪЪЕБТЗОЖдЫЖЏЕН![]() жсЩЯЕФФГИіЕуGДІЃЌдйбиЪЪЕБТЗОЖдЫЖЏЕН
жсЩЯЕФФГИіЕуGДІЃЌдйбиЪЪЕБТЗОЖдЫЖЏЕН![]() жсЩЯЕФФГИіЕуHДІЃЌзюКѓЕНДяЯпЖЮBCЕФжаЕуFДІЭЃжЙЃЌЧѓЕБЁїPCBУцЛ§зюДѓЪБЃЌЕуPЕФзјБъМАЕуQдкећИідЫЖЏЙ§ГЬжаОЙ§ЕФзюЖЬТЗОЖЕФГЄЃЛ
жсЩЯЕФФГИіЕуHДІЃЌзюКѓЕНДяЯпЖЮBCЕФжаЕуFДІЭЃжЙЃЌЧѓЕБЁїPCBУцЛ§зюДѓЪБЃЌЕуPЕФзјБъМАЕуQдкећИідЫЖЏЙ§ГЬжаОЙ§ЕФзюЖЬТЗОЖЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЁїPCBУцЛ§зюДѓЪБЃЌАбХзЮяЯп![]() ЯђгвЦНвЦЪЙЫќЕФЭМЯѓОЙ§ЕуPЃЌЕУЕНаТХзЮяЯп
ЯђгвЦНвЦЪЙЫќЕФЭМЯѓОЙ§ЕуPЃЌЕУЕНаТХзЮяЯп![]() ЃЌдкаТХзЮяЯп
ЃЌдкаТХзЮяЯп![]() ЩЯЃЌЪЧЗёДцдкЕуEЃЌЪЙЁїECBЕФУцЛ§ЕШгкЁїPCBЕФУцЛ§ЃЎШєДцдкЃЌЧыЧѓГіЕуEЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЩЯЃЌЪЧЗёДцдкЕуEЃЌЪЙЁїECBЕФУцЛ§ЕШгкЁїPCBЕФУцЛ§ЃЎШєДцдкЃЌЧыЧѓГіЕуEЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉЕуQАДеевЊЧѓОЙ§ЕФзюЖЬТЗОЖГЄЮЊ
ЃЈ2ЃЉЕуQАДеевЊЧѓОЙ§ЕФзюЖЬТЗОЖГЄЮЊ![]() ЃЈ3ЃЉДцдкЃЌТњзуЬѕМўЕФЕуEгаШ§ИіЃЌМДЃЈ
ЃЈ3ЃЉДцдкЃЌТњзуЬѕМўЕФЕуEгаШ§ИіЃЌМДЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ, ЃЈ
ЃЉ, ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЕУГіНсТлЃЛ
ЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЯШШЗЖЈГі![]() ЃЌдйРћгУШ§НЧаЮЕФУцЛ§ЙЋЪНЕУГі
ЃЌдйРћгУШ§НЧаЮЕФУцЛ§ЙЋЪНЕУГі![]() ЃЌМДПЩЕУГіНсТлЃЛ
ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШШЗЖЈГіЦНвЦКѓЕФХзЮяЯпНтЮіЪНЃЌНјЖјЧѓГі![]() ЃЌдкХаЖЯГі
ЃЌдкХаЖЯГі![]() НЈСЂЗНГЬМДПЩЕУГіНсТлЃЎ
НЈСЂЗНГЬМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉСю![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Ёр AЃЈ![]() ЃЌ0ЃЉЃЌBЃЈ
ЃЌ0ЃЉЃЌBЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
Сю![]() ЃЌЕУ
ЃЌЕУ![]() ЃЎ
ЃЎ
ЁрC(0,3)ЃЎ
ЩшжБЯпBCЕФКЏЪ§БэДяЪНЮЊ![]() ЃЌАбBЃЈ
ЃЌАбBЃЈ![]() ЃЌ0ЃЉДњШыЃЌЕУ
ЃЌ0ЃЉДњШыЃЌЕУ![]() ЃЎ
ЃЎ
НтЕУЃЌ![]() ЃЎ
ЃЎ
ЫљвджБЯпBCЕФКЏЪ§БэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЙ§PзїPDЁЭ![]() жсНЛжБЯпBCгкMЃЎ
жсНЛжБЯпBCгкMЃЎ
Ёп жБЯпBCБэДяЪНЮЊ ![]() ЃЌ
ЃЌ
ЩшЕуMЕФзјБъЮЊ![]() ЃЌдђЕуP ЕФзјБъЮЊ
ЃЌдђЕуP ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
дђ![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ЁрДЫЪБЃЌЕуPзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ИљОнЬтвтЃЌвЊЧѓЕФЯпЖЮPG+GH+HFЕФзюаЁжЕЃЌжЛашвЊАбетШ§ЬѕЯпЖЮЁААсЁБдквЛжБЯпЩЯЃЎШчЭМ1ЃЌзїЕуPЙигк![]() жсЕФЖдГЦЕу
жсЕФЖдГЦЕу![]() ЃЌзїЕуFЙигк
ЃЌзїЕуFЙигк![]() жсЕФЖдГЦЕу
жсЕФЖдГЦЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕуG,НЛ
жсгкЕуG,НЛ![]() жсгкЕуHЃЎИљОнжсЖдГЦадПЩЕУ
жсгкЕуHЃЎИљОнжсЖдГЦадПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ДЫЪБPG+GH+HFЕФзюаЁжЕ=![]() ЃЎ
ЃЎ

Ёп ЕуPзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЁр Еу
ЃЉЃЌЁр Еу![]() ЕФзјБъЮЊЃЈ
ЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
Ёп ЕуFЪЧЯпЖЮBCЕФжаЕуЃЌ
Ёр ЕуFЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
Ёр Еу![]() ЕФзјБъЮЊЃЈ
ЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
Ёп Еу![]() ЃЌPСНЕуЕФКсзјЯрЭЌЃЌЁр
ЃЌPСНЕуЕФКсзјЯрЭЌЃЌЁр![]() ЁЭ
ЁЭ![]() жсЃЎ
жсЃЎ
Ёп ![]() ЃЌPСНЕуЙигк
ЃЌPСНЕуЙигк![]() жсЖдГЦЃЌЁр
жсЖдГЦЃЌЁр![]() ЁЭ
ЁЭ![]() жсЃЎ
жсЃЎ
Ёр ![]() ЃЎ
ЃЎ
Ёр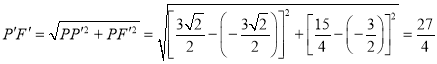 ЃЎ
ЃЎ
МДЕуQАДеевЊЧѓОЙ§ЕФзюЖЬТЗОЖГЄЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌдкХзЮяЯп![]() жаЃЌ
жаЃЌ
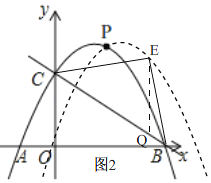
Сю![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЃЌ
ЃЌ
гЩЦНвЦжЊЃЌХзЮяЯп![]() ЯђгвЦНвЦЕН
ЯђгвЦНвЦЕН![]() ЃЌдђЦНвЦСЫ
ЃЌдђЦНвЦСЫ![]() ИіЕЅЮЛЃЌ
ИіЕЅЮЛЃЌ![]() ЃЌ
ЃЌ
ЩшЕу![]() ЃЌ
ЃЌ
Й§Еу![]() зї
зї![]() жсНЛ
жсНЛ![]() гк
гк![]() ЃЌ
ЃЌ
![]() жБЯп
жБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]()
![]() ЕФУцЛ§ЕШгк
ЕФУцЛ§ЕШгк![]() ЕФУцЛ§ЃЌ
ЕФУцЛ§ЃЌ
![]() ЃЌ
ЃЌ
гЩЃЈ2ЃЉжЊЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЈЩс
ЃЈЩс![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуEгаШ§ИіЃЌМДЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ, ЃЈ
ЃЉ, ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ


 гХМгОЋОэЯЕСаД№АИ
гХМгОЋОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
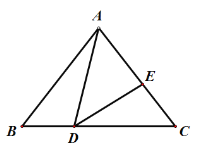
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌAB=AC=6ЃЌBC=8ЃЌЕуDЁЂEЗжБ№дкBCЃЌACЩЯЃЌЧвЁЯADE=ЁЯBЃЌШєЁїADEЪЧЕШбќШ§НЧаЮЃЌдђBDЕФГЄЮЊ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() ЩЯвРДЮга
ЩЯвРДЮга![]() Ш§ЕуЃЌ
Ш§ЕуЃЌ![]() ЕФбгГЄЯпНЛ
ЕФбгГЄЯпНЛ![]() гк
гк![]() Й§Еу
Й§Еу![]() зї
зї![]() НЛ
НЛ![]() ЕФбгГЄЯпгк
ЕФбгГЄЯпгк![]() СЌ
СЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
ЃЈ2ЃЉСЌНг![]()
![]() ЕБ
ЕБ![]()
![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЮЊЛЁ
ЮЊЛЁ![]() ЕФжаЕуЃЛ
ЕФжаЕуЃЛ
![]() Шє
Шє![]() Чв
Чв![]() ЃЌдђ
ЃЌдђ![]() ЕФАыОЖЪЧ ЃЎ
ЕФАыОЖЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАаЃдААВШЋЁБЪмЕНЩчЛсЕФЙуЗКЙизЂЃЌФГаЃеўНЬДІЖдВПЗжбЇЩњОЭаЃдААВШЋжЊЪЖЕФСЫНтГЬЖШЃЌНјааСЫЫцЛњГщбљЕїВщЃЌВЂЛцжЦСЫШчЯТСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЎЧыФуИљОнЭГМЦЭМжаЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
(1)НгЪмЮЪОэЕїВщЕФбЇЩњЙВга______УћЃЛ
(2)ЧыВЙШЋелЯпЭГМЦЭМЃЌВЂЧѓГіЩШаЮЭГМЦЭМжаЁАЛљБОСЫНтЁБВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЕФДѓаЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
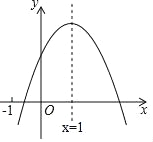
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгыxжсНЛгкЃЈx1ЃЌ0ЃЉЃЌЧвЉ1ЃМx1ЃМ0ЃЌЖдГЦжсxЃН1ЃЎШчЭМЫљЪОЃЌгаЯТСа5ИіНсТлЃКЂйabcЃО0ЃЛЂкbЃМa+cЃЛЂл4a+2b+cЃО0ЃЛЂм2cЃМ3bЃЛЂнa+bЃОmЃЈam+bЃЉЃЈmЁй1ЕФЪЕЪ§ЃЉЃЎЦфжаЫљгаНсТле§ШЗЕФЪЧ______ЃЈЬюаДЗЌКХЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃК
ЖдгкСНИіе§Ъ§aЁЂbЃЌдђ![]() ЃЈЕБЧвНіЕБaЃНbЪБШЁЕШКХЃЉЃЎ
ЃЈЕБЧвНіЕБaЃНbЪБШЁЕШКХЃЉЃЎ
ЕБ![]() ЮЊЖЈжЕЪБЃЌ
ЮЊЖЈжЕЪБЃЌ![]() газюаЁжЕЃЛЕБ
газюаЁжЕЃЛЕБ![]() ЮЊЖЈжЕЪБЃЌ
ЮЊЖЈжЕЪБЃЌ![]() газюДѓжЕЃЎ
газюДѓжЕЃЎ
Р§ШчЃКвбжЊ![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
НтЃКгЩ![]() Ён
Ён![]() ЃЌЕУ
ЃЌЕУ![]() Ён
Ён![]() ЃЌЕБЧвНіЕБ
ЃЌЕБЧвНіЕБ![]() МД
МД![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЮЊ
газюаЁжЕЃЌзюаЁжЕЮЊ![]() ЃЎ
ЃЎ
ИљОнЩЯУцЕФдФЖСВФСЯЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉвбжЊ![]() ЃЌШє
ЃЌШє![]() ЃЌдђЕБ
ЃЌдђЕБ![]() ЁЁЪБЃЌ
ЁЁЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЮЊ ЁЁЃЛ
газюаЁжЕЃЌзюаЁжЕЮЊ ЁЁЃЛ
ЃЈ2ЃЉвбжЊ![]() ЃЌШє
ЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ШЁКЮжЕЪБЃЌ
ШЁКЮжЕЪБЃЌ![]() газюаЁжЕЃЌзюаЁжЕЪЧЖрЩйЃП
газюаЁжЕЃЌзюаЁжЕЪЧЖрЩйЃП
ЃЈ3ЃЉгУГЄЮЊ![]() РщАЪЮЇвЛИіГЄЗНаЮЛЈдАЃЌЮЪетИіГЄЗНаЮЛЈдАЕФГЄЁЂПэИїЮЊЖрЩйЪБЃЌЫљЮЇЕФГЄЗНаЮЛЈдАУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧЖрЩйЃП
РщАЪЮЇвЛИіГЄЗНаЮЛЈдАЃЌЮЪетИіГЄЗНаЮЛЈдАЕФГЄЁЂПэИїЮЊЖрЩйЪБЃЌЫљЮЇЕФГЄЗНаЮЛЈдАУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСвдЯТВФСЯЃКЖдЪ§ЕФДДЪМШЫЪЧЫеИёРМЪ§бЇМвФЩЦЄЖћЃЈJЃЎNapierЃЌ1550Фъ-1617ФъЃЉЃЌФЩЦЄЖћЗЂУїЖдЪ§ЪЧдкжИЪ§ИХФюНЈСЂжЎЧАЃЌжБЕН18ЪРМЭШ№ЪПЪ§бЇМвХЗРЃЈEulerЃЌ1707Фъ-1783ФъЃЉВХЗЂЯжжИЪ§гыЖдЪ§жЎМфЕФСЊЯЕЃЎЖдЪ§ЕФЖЈвхЃКвЛАуЕиЃЌШє![]() ЃЌдђ
ЃЌдђ![]() Назівд
Назівд![]() ЮЊЕз
ЮЊЕз![]() ЕФЖдЪ§ЃЌМЧзї
ЕФЖдЪ§ЃЌМЧзї![]() ЃЎБШШчжИЪ§ЪН
ЃЎБШШчжИЪ§ЪН![]() ПЩвдзЊЛЏЮЊ
ПЩвдзЊЛЏЮЊ![]() ЃЌЖдЪ§ЪН
ЃЌЖдЪ§ЪН![]() ПЩвдзЊЛЏЮЊ
ПЩвдзЊЛЏЮЊ![]() ЃЎЮвУЧИљОнЖдЪ§ЕФЖЈвхПЩЕУЕНЖдЪ§ЕФвЛИіаджЪЃК
ЃЎЮвУЧИљОнЖдЪ§ЕФЖЈвхПЩЕУЕНЖдЪ§ЕФвЛИіаджЪЃК![]()
![]() ЃЎРэгЩШчЯТЃКЩш
ЃЎРэгЩШчЯТЃКЩш![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌгЩЖдЪ§ЕФЖЈвхЕУ
ЃЌгЩЖдЪ§ЕФЖЈвхЕУ![]() ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЎНтОівдЯТЮЪЬтЃК
ЃЎНтОівдЯТЮЪЬтЃК
ЃЈ1ЃЉНЋжИЪ§![]() зЊЛЏЮЊЖдЪ§ЪНЃК ЃЎ
зЊЛЏЮЊЖдЪ§ЪНЃК ЃЎ
ЃЈ2ЃЉЗТееЩЯУцЕФВФСЯЃЌЪджЄУїЃК![]()
ЃЈ3ЃЉЭиеЙдЫгУЃКМЦЫу![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
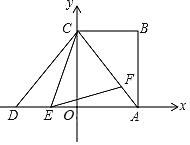
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDЕФЖЅЕуAЁЂCдкЦНУцжБНЧзјБъЯЕЕФзјБъжсЩЯЃЌABЃН4ЃЌCBЃН3ЃЌЕуDгыЕуAЙигкyжсЖдГЦЃЌЕуEЁЂFЗжБ№ЪЧЯпЖЮDAЁЂACЩЯЕФЖЏЕуЃЈЕуEВЛгыAЁЂDжиКЯЃЉЃЌЧвЁЯCEFЃНЁЯACBЃЌШєЁїEFCЮЊЕШбќШ§НЧаЮЃЌдђЕуEЕФзјБъЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКЮвУЧжЊЕРЃЌЫФБпаЮЕФвЛЬѕЖдНЧЯпАбетИіЫФБпаЮЗжГЩСЫСНИіШ§НЧаЮЃЌШчЙћетСНИіШ§НЧаЮЯрЫЦЃЈВЛШЋЕШЃЉЃЌЮвУЧОЭАбетЬѕЖдНЧЯпНазіетИіЫФБпаЮЕФЁАЯрЫЦЖдНЧЯпЁБЃЛ
РэНтЃК
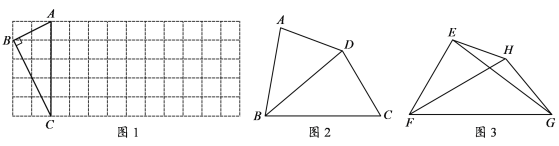
ЂХ ШчЭМ1ЃЌЁїABCЕФШ§ИіЖЅЕуОљдке§ЗНаЮЭјИёжаЕФИёЕуЩЯЃЌШєЫФБпаЮABCDЪЧвдACЮЊЁАЯрЫЦЖдНЧЯпЁБЕФЫФБпаЮЃЌЧыгУЮоПЬЖШЕФжБГпдкЭјИёжаЛГіЕуDЃЈБЃСєЛЭМКлМЃЃЌевГі3ИіМДПЩЃЉЃЛ
ЂЦ ШчЭМ2ЃЌдкЫФБпаЮABCDжаЃЌЁЯABCЃН80ЁуЃЌЁЯADCЃН140ЁуЃЌЖдНЧЯпBDЦНЗжЁЯABC. ЧыЮЪBDЪЧЫФБпаЮABCDЕФЁАЯрЫЦЖдНЧЯпЁБТ№ЃПЧыЫЕУїРэгЩЃЛ
дЫгУЃК
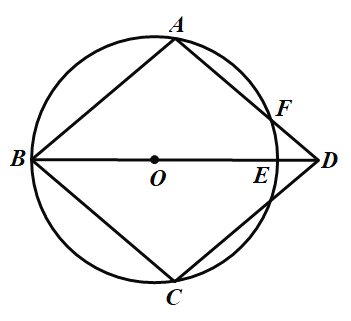
ЂЧ ШчЭМ3ЃЌвбжЊFHЪЧЫФБпаЮEFGHЕФЁАЯрЫЦЖдНЧЯпЁБЃЌ ЁЯEFHЃНЁЯHFGЃН30Ёу.СЌНгEGЃЌШєЁїEFGЕФУцЛ§ЮЊ![]() ЃЌЧѓFH ЕФГЄ.
ЃЌЧѓFH ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com