
【题目】如图,在![]() 上依次有
上依次有![]() 三点,
三点,![]() 的延长线交
的延长线交![]() 于
于![]() 过点
过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() 连
连![]() 交
交![]() 于点
于点![]() .
.
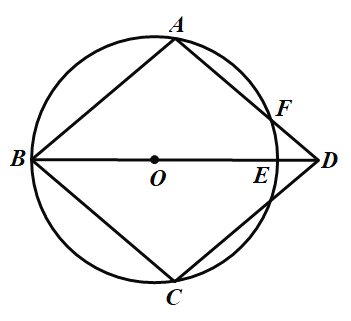
(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]()
![]() 当
当![]()
![]() 时,点
时,点![]() 为弧
为弧![]() 的中点;
的中点;
![]() 若
若![]() 且
且![]() ,则
,则![]() 的半径是 .
的半径是 .
【答案】(1)见解析;(2)①72°,②3
【解析】
(1) 先由一组对边平行且相等可得四边形ABCD是平行四边形,再结合AB=BC证明是菱形;
(2)![]() 由点
由点![]() 为弧
为弧![]() 的中点推出∠AOF=∠EOF= m,设参数表示△OFA各个角,根据三角形内角和列方程计算即可;
的中点推出∠AOF=∠EOF= m,设参数表示△OFA各个角,根据三角形内角和列方程计算即可;
![]() 由
由![]() 设参数证明△AOF是等边三角形即可.
设参数证明△AOF是等边三角形即可.
(1)证明:∵![]() ,
,
∴∠CBD=∠ABD,
∵CD∥AB,
∴∠ABD=∠CDB,
∴∠CBD=∠CDB,
∴CB=CD,
∵BE是⊙O的直径,
∴![]() ,
,
∴AB=BC=CD,
∵CD∥AB,
∴四边形ABCD是菱形;
(2)①F为弧AE的中点,设∠AOF=∠EOF= m
∴∠ABE=∠ADE=m
∴∠OAF=∠OFA=2m
∵∠AOF+∠OAF+∠OFA=180°
∴2m+2m+m=180°
∴m=36°
∴∠ABE=72°
②∵∠AOF=3∠FOE,
设∠FOE=x,则∠AOF=3x,
∠AOD=∠FOE+∠AOF=4x,
∵OA=OF,
∴∠OAF=∠OFA=![]() (180﹣3x)°,
(180﹣3x)°,
∵OA=OB,
∴∠OAB=∠OBA=2x,
∴∠ABC=4x,
∵BC∥AD,
∴∠ABC+∠BAD=180°,
∴4x+2x+![]() (180﹣3x)=180,
(180﹣3x)=180,
x=20°,
∴∠AOF=3x=60°,
∵OA=OF,
∴△AOF是等边三角形,
∴OF=AF=3,


图(1) 图(2)


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
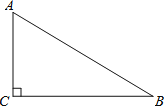
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边AB上求作一点P,使PC=PB,并连接PC;(不写作法,保留作图痕迹)
(2)当AC=3,BC=4时,△ACP的周长= ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店每天售出甲、乙两种笔,统计后发现:甲、乙两种笔同一天售出量之间满足一次函数的关系,设甲、乙两种笔同一天的售出量分别为x(支)、y(支),部分数据如表所示(下表中每一列数据表示甲、乙两种笔同一天的售出量).
甲种笔售出x(支) | … | 4 | 6 | 8 | … |
乙种笔售出y(支) | … | 6 | 12 | 18 | … |
(1)求y关于x的函数关系式;(不需要写出函数的定义域)
(2)某一天文具店售出甲、乙两种笔的营业额分别为30元和120元,如果乙种笔每支售价比甲种笔每支售价多2元,那么甲、乙两种笔这天各售出多少支?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
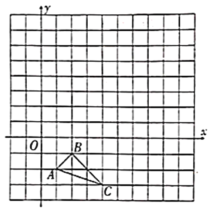
(2)以点![]() 为位似中心,在网格中画出
为位似中心,在网格中画出![]() 的位似图形
的位似图形![]() ,使
,使![]() 与
与![]() 的相似比为
的相似比为![]() .
.
(3)设点![]() 为
为![]() 内一点,则依上述两次变换后,点
内一点,则依上述两次变换后,点![]() 在
在![]() 内的对应点
内的对应点![]() 的坐标是_____.
的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越野自行车是中学生喜爱的交通工具,市场巨大竞争也激烈.某品牌经销商经营的A型车去年销售总额为5万元,今年每辆售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.B型车是今年增加供应市场的,功能多售价也高些.
A、B两种型号车今年的进货和销售价格如下表:
A型车 | B型车 | |
进货价 | 1100元/辆 | 1400元/辆 |
销售价 | x元/辆 | 2000元/辆 |
(1)求今年A型车每辆销售价x的值;
(2)该品牌经销商计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,请问应如何安排两种型号车的进货数量,才能使这批车售出后获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
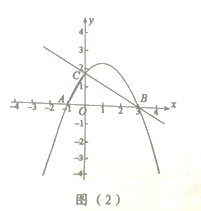
【题目】如图1,在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过
经过![]() 三点,且其对称轴为
三点,且其对称轴为![]() 其中点
其中点![]() ,点
,点![]() .
.

(1)求抛物线的解析式;
(2)①如图(1),点![]() 是直线
是直线![]() 上方抛物线上的动点,当四边形
上方抛物线上的动点,当四边形![]() 的面积取最大值时,求点
的面积取最大值时,求点![]() 的坐标;
的坐标;
②如图(2),连接![]() 在抛物线上有一点
在抛物线上有一点![]() 满足
满足![]() ,请直接写出点
,请直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3cm、AC=4cm、BC=5cm,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画的条数为( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C,连接BC.
轴交于点C,连接BC.
(1)如图1,求直线BC的表达式;
(2)如图1,点P是抛物线上位于第一象限内的一点,连接PC,PB,当△PCB面积最大时,一动点Q从点P从出发,沿适当路径运动到![]() 轴上的某个点G处,再沿适当路径运动到
轴上的某个点G处,再沿适当路径运动到![]() 轴上的某个点H处,最后到达线段BC的中点F处停止,求当△PCB面积最大时,点P的坐标及点Q在整个运动过程中经过的最短路径的长;
轴上的某个点H处,最后到达线段BC的中点F处停止,求当△PCB面积最大时,点P的坐标及点Q在整个运动过程中经过的最短路径的长;
(3)如图2,在(2)的条件下,当△PCB面积最大时,把抛物线![]() 向右平移使它的图象经过点P,得到新抛物线
向右平移使它的图象经过点P,得到新抛物线![]() ,在新抛物线
,在新抛物线![]() 上,是否存在点E,使△ECB的面积等于△PCB的面积.若存在,请求出点E的坐标,若不存在,请说明理由.
上,是否存在点E,使△ECB的面积等于△PCB的面积.若存在,请求出点E的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
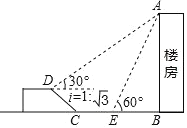
【题目】如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面![]() 处测得楼房顶部
处测得楼房顶部![]() 的仰角为
的仰角为![]() ,沿坡面向下走到坡脚
,沿坡面向下走到坡脚![]() 处,然后向楼房方向继续行走10米到达
处,然后向楼房方向继续行走10米到达![]() 处,测得楼房顶部
处,测得楼房顶部![]() 的仰角为
的仰角为![]() .已知坡面
.已知坡面![]() 米,山坡的坡度
米,山坡的坡度![]() (坡度
(坡度![]() 是指坡面的铅直高度与水平宽度的比),求楼房
是指坡面的铅直高度与水平宽度的比),求楼房![]() 高度.(结果精确到0.1米)(参考数据:
高度.(结果精确到0.1米)(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com