
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
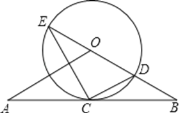
(1)求证:直线AB是⊙O的切线;
(2)试猜想BC,BD,BE三者之间的等量关系,并加以证明;
(3)若tan∠CED=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
【答案】(1)见解析;(2)BC2=BDBE,证明见解析;(3)5
【解析】
(1)连接OC,根据等腰三角形的性质易得OC⊥AB;即可得到证明;
(2)易得∠BCD=∠E,又有∠CBD=∠EBC,可得△BCD∽△BEC;故可得BC2=BDBE;
(3)易得△BCD∽△BEC,BD=x,由三角形的性质,易得BC2=BDBE,代入数据即可求出答案.
(1)证明:如图,连接OC,
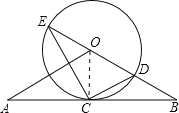
∵OA=OB,CA=CB,
∴OC⊥AB,
∴AB是⊙O的切线.
(2)解:BC2=BDBE.
证明:∵ED是直径,
∴∠ECD=90°,
∴∠E+∠EDC=90°.
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC(OC=OD),
∴∠BCD=∠E.
又∵∠CBD=∠EBC,
∴△BCD∽△BEC.
∴![]() .
.
∴BC2=BDBE.
(3)解:∵tan∠CED=![]() ,
,
∴![]() .
.
∵△BCD∽△BEC,
∴![]() .
.
设BD=x,则BC=2x,
∵BC2=BDBE,
∴(2x)2=x(x+6).
∴x1=0,x2=2.
∵BD=x>0,
∴BD=2.
∴OA=OB=BD+OD=3+2=5.


科目:初中数学 来源: 题型:
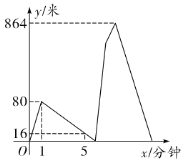
【题目】疫情之下,中华儿女共抗时艰.重庆和湖北同饮长江水,为更好地驰援武汉,打赢防疫攻坚战,我市某公益组织收集社会捐献物资.甲、乙两人先后从![]() 地沿相同路线出发徒步前往
地沿相同路线出发徒步前往![]() 地进行物资捐献,甲出发1分钟后乙再出发,一段时间后乙追上甲,这时甲发现有东西落在
地进行物资捐献,甲出发1分钟后乙再出发,一段时间后乙追上甲,这时甲发现有东西落在![]() 地,于是原路原速返回
地,于是原路原速返回![]() 地去取(甲取东西的时间忽略不计),而乙继续前行,甲乙两人到达B地后原地帮忙.已知在整个过程中,甲乙均保持各自的速度匀速行走,甲、乙两人相距的路程
地去取(甲取东西的时间忽略不计),而乙继续前行,甲乙两人到达B地后原地帮忙.已知在整个过程中,甲乙均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分钟)之间的函数关系如图所示,则当乙到达
(分钟)之间的函数关系如图所示,则当乙到达![]() 地时,甲距
地时,甲距![]() 地的路程是_______米.
地的路程是_______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
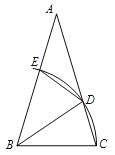
【题目】如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,BC长为半径的弧分别交AC,AB于点D,E,连接BD,ED.
(1)写出图中所有的等腰三角形;
(2)若∠AED=114°,求∠ABD和∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在射线
在射线![]() 上(不与点
上(不与点![]() 、点
、点![]() 重合),将线段
重合),将线段![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,作射线
,作射线![]() 与射线
与射线![]() ,两射线交于点
,两射线交于点![]() .
.
(1)若点![]() 在线段
在线段![]() 上,如图1,请直接写出
上,如图1,请直接写出![]() 与
与![]() 的关系.
的关系.
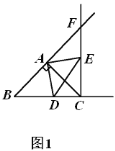
(2)若点![]() 在线段
在线段![]() 的延长线上,如图2,(1)中的结论还成立吗?请说明理由.
的延长线上,如图2,(1)中的结论还成立吗?请说明理由.

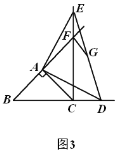
(3)在(2)的条件下,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店每天售出甲、乙两种笔,统计后发现:甲、乙两种笔同一天售出量之间满足一次函数的关系,设甲、乙两种笔同一天的售出量分别为x(支)、y(支),部分数据如表所示(下表中每一列数据表示甲、乙两种笔同一天的售出量).
甲种笔售出x(支) | … | 4 | 6 | 8 | … |
乙种笔售出y(支) | … | 6 | 12 | 18 | … |
(1)求y关于x的函数关系式;(不需要写出函数的定义域)
(2)某一天文具店售出甲、乙两种笔的营业额分别为30元和120元,如果乙种笔每支售价比甲种笔每支售价多2元,那么甲、乙两种笔这天各售出多少支?
查看答案和解析>>
科目:初中数学 来源: 题型:
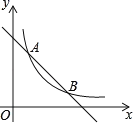
【题目】已知反比例函数y=![]() 与一次函数y=ax+b的图象相交于点A(2,6),和点B(4,m).
与一次函数y=ax+b的图象相交于点A(2,6),和点B(4,m).
(1)求反比例函数与一次函数的解析式;
(2)直接写出不等式![]() ≤ax+b的解集和△AOB的面积.
≤ax+b的解集和△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越野自行车是中学生喜爱的交通工具,市场巨大竞争也激烈.某品牌经销商经营的A型车去年销售总额为5万元,今年每辆售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.B型车是今年增加供应市场的,功能多售价也高些.
A、B两种型号车今年的进货和销售价格如下表:
A型车 | B型车 | |
进货价 | 1100元/辆 | 1400元/辆 |
销售价 | x元/辆 | 2000元/辆 |
(1)求今年A型车每辆销售价x的值;
(2)该品牌经销商计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,请问应如何安排两种型号车的进货数量,才能使这批车售出后获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个四边形的对角线把四边形分成两个三角形,一个是等边三角形,另一个是该对角线所对的角为![]() 的三角形,我们把这条对角线叫做这个四边形的理想对角线,这个四边形称为理想四边形.
的三角形,我们把这条对角线叫做这个四边形的理想对角线,这个四边形称为理想四边形.
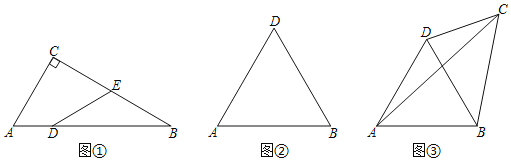
(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,求证:四边形
,求证:四边形![]() 为理想四边形;
为理想四边形;
(2)如图②,![]() 是等边三角形,若
是等边三角形,若![]() 为理想对角线,四边形
为理想对角线,四边形![]() 为理想四边形.请画图找出符合条件的C点落在怎样的图形上;(在图中标出必要的数据)
为理想四边形.请画图找出符合条件的C点落在怎样的图形上;(在图中标出必要的数据)
(3)在(2)的条件下,
①若![]() 为直角三角形,
为直角三角形,![]() ,求
,求![]() 的长度;
的长度;
②如图③,若![]() ,
,![]() ,
,![]() ,请直接写出
,请直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com