
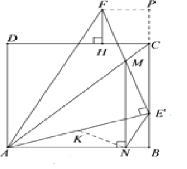
【题目】如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.


(1)求证:AE=![]() NE+ME;
NE+ME;
(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.猜想CH与FH存在的数量关系,并证明你的结论;
【答案】(1)详见解析;(2)CH=FH,详见解析;
【解析】
(1)过点N作NK⊥NE,交AE于点K,由“ASA”可证△ANK≌△MNE,可证AE=![]() NE+ME;
NE+ME;
(2)过点F作FP⊥BC,交BC的延长线于点P,利用正方形的性质AAS证明△ABE≌△EPF,即可解答;
(1)证明:过点N作NK⊥NE,交AE于点K.
∴∠KNE=90°.
∵MN⊥AB,∴∠MNA=90°.
∴∠ANK=∠MNE.
∵ME⊥AE,∴∠AEM=∠ANM=90°.
∴∠NAK=∠NME.
∵四边形ABCD是正方形,∠ANM=90°.
∴∠MAN=∠NMA=45°.
∴AN=MN.
在△ANK和△MNE中,
∵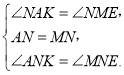
∴△ANK≌△MNE.
∴AK=ME,NK=NE.
∴ KE=![]() NE.
NE.
∴ AE=AK+KE=ME+![]() NE.
NE.
解:(2)CH=FH.
过点F作FP⊥BC,交BC的延长线于点P.
∴∠P=90°.
∵∠BAE+∠AEB=∠FEP+∠AEB=90°,
∴∠BAE=∠FEP.
∵四边形ABCD是正方形,
∴∠B=∠BCD=∠PCD= 90°,AB=BC.
∵FH⊥CD,∴∠FHC=90°.
∴∠P=∠PCH=∠CHF=90°.
∴四边形PCHF是矩形.
在△ABE和△EPF中,
∵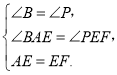
∴△ABE≌△EPF.
∴BE=PF,AB=EP.
∵AB=BC,
∴EP=BC.
∴CP=BE=PF.
∴矩形PCHF是正方形.
∴FH=CH.


科目:初中数学 来源: 题型:
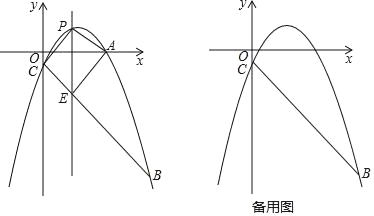
【题目】如图,已知抛物线y=﹣![]() x2+bx+c经过点A(5,
x2+bx+c经过点A(5,![]() )、点B(9,﹣10),与y轴交于点C,点P是直线AC上方抛物线上的一个动点;
)、点B(9,﹣10),与y轴交于点C,点P是直线AC上方抛物线上的一个动点;
(1)求抛物线对应的函数解析式;
(2)过点P且与y轴平行的直线l与直线BC交于点E,当四边形AECP的面积最大时,求点P的坐标;
(3)当∠PCB=90°时,作∠PCB的角平分线,交抛物线于点F.
①求点P和点F的坐标;
②在直线CF上是否存在点Q,使得以F、P、Q为顶点的三角形与△BCF相似,若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
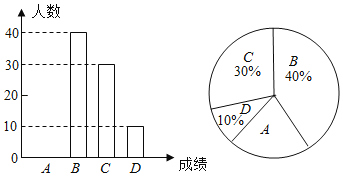
【题目】我校为了了解九年级学生身体素质测试情况,随机抽取了本校九年级部分学生的身体素质测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如图不完整的统计图,请你结合图表所给信息解答下列问题:
(1)请在答题卡上直接将条形统计图补充完整;
(2)扇形统计图中“B”部分所对应的圆心角的度数是 °;
(3)若我校九年级共有1500名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
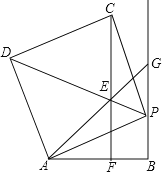
【题目】如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经历疫情复学后,学校开展了多种形式的防疫知识讲座,并举行了全员参加的“防疫”知识竞赛,试卷题目共10题,每题10分.现分别从七年级1,2,3班中各随机抽取10名同学的成绩(单位:分).
收集整理数据如下:
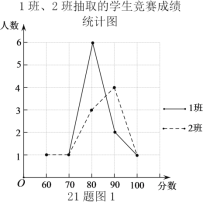
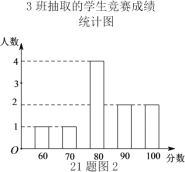
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 |
| 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由(一条理由即可);
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级学生共120人,试估计需要准备多少张奖状?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AB=4,点C是AB延长线上一点,且BC=2,点D是半圆的中点,点P是⊙O上任意一点.
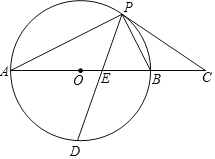
(1)当PD与AB交于点E且PC=CE时,求证:PC与⊙O相切;
(2)在(1)的条件下,求PC的长;
(3)点P是⊙O上动点,当PD+PC的值最小时,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
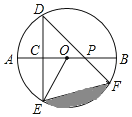
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段公路施工,甲工程队单独施工完成的天数是乙工程队单独施工完天数的2倍,由甲、乙两工程队合作20天可完成,.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)若此项过程由甲工程队单独施工,再由甲、乙两工程队合作施工完成剩下的工程,已知甲工程队每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,要使施工费用不超过64万元,则甲工程队至少要单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
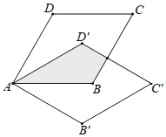
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,则图中阴影部分的面积为( )
A.1+![]() B.2+
B.2+![]()
C.3D.3–![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com