
【题目】如图,已知AB是⊙O的直径,AB=4,点C是AB延长线上一点,且BC=2,点D是半圆的中点,点P是⊙O上任意一点.
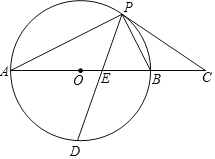
(1)当PD与AB交于点E且PC=CE时,求证:PC与⊙O相切;
(2)在(1)的条件下,求PC的长;
(3)点P是⊙O上动点,当PD+PC的值最小时,求PC的长.
【答案】(1)详见解析;(2)2![]() ;(3)
;(3)![]()
【解析】
(1)根据点D是半圆的中点可得,∠APD=45°,根据圆的半径相等和三角形的外角性质可推出∠PEC=90°﹣∠OPE,根据PC=CE即可证得;
(2)在△OPC中,由勾股定理即可求出PC的长;
(3)根据两点之间线段最短可知,当点C、P、D三点共线时,PD+PC最小,根据圆内接四边形的性质和已知条件可证得△CBP'∽△CDA,利用对应边成比例即可求出答案.
(1)证明:如图1,
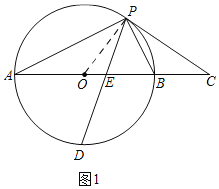
∵点D是半圆的中点,
∴∠APD=45°,
连接OP,
∴OA=OP,
∴∠OAP=∠OPA,
∴∠PEC=∠OAP+∠APE=∠OPA+∠APE=∠APE﹣∠OPE+∠APE=2∠APE﹣∠OPE=90°﹣∠OPE,
∵PC=EC,
∴∠CPE=∠PEC=90°﹣∠APE,
∴∠OPC=∠OPE+∠CPE=∠OPE+90°﹣∠OPE=90°,
∵点P在⊙O上,
∴PC是⊙O的切线;
(2)解:由(1)知,∠OPC=90°,
∵AB=4,
∴OP=OB=![]() AB=2,
AB=2,
∵BC=2,
∴OC=OB+BC=4,
根据勾股定理得,![]() ;
;
(3)解:连接OD,如图2,
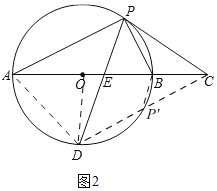
∵D是半圆O的中点,
∴∠BOD=90°,要使PD+PC的值最小,则连接CD交⊙O于P',
即点P在P'的位置时,PD+PC最小,
由(2)知,OC=4,
在Rt△COD中,OD=OB=2,
根据勾股定理得,![]() ,
,
连接BP,AD,则四边形ADP'B是⊙O的内接四边形,
∴∠CBP'=∠CDA,
∵∠BCP=∠DCA,
∴△CBP'∽△CDA,
∴![]() ,
,
∴![]() ,
,
∴CP'=![]() ,
,
∴当PD+PC的值最小时,PC=![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
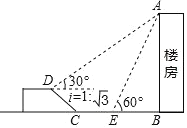
【题目】如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面![]() 处测得楼房顶部
处测得楼房顶部![]() 的仰角为
的仰角为![]() ,沿坡面向下走到坡脚
,沿坡面向下走到坡脚![]() 处,然后向楼房方向继续行走10米到达
处,然后向楼房方向继续行走10米到达![]() 处,测得楼房顶部
处,测得楼房顶部![]() 的仰角为
的仰角为![]() .已知坡面
.已知坡面![]() 米,山坡的坡度
米,山坡的坡度![]() (坡度
(坡度![]() 是指坡面的铅直高度与水平宽度的比),求楼房
是指坡面的铅直高度与水平宽度的比),求楼房![]() 高度.(结果精确到0.1米)(参考数据:
高度.(结果精确到0.1米)(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】思维探索:
在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
(1)如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是 ;
(2)如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;
拓展提升:
如图3,在Rt△ABC中,∠ACB=90°,CA=CB,过点B作BD⊥BC,连接AD,在BC的延长线上取一点E,使∠EDA=30°,连接AE,当BD=2,∠EAD=45°时,请直接写出线段CE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,某地的计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 2元/公里 |
| 1元/公里 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收1元. | |||
小李与小张分别从不同地点,各自同时乘坐滴滴快车,到同一地点相见,已知到达约定地点时他们的实际行车里程分别为7公里与9公里,两人付给滴滴快车的乘车费相同.其中一人先到达约定地点,他等候另一人的时间等于他自己实际乘车时间,且恰好是另一人实际乘车时间的一半,则小李的乘车费为______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.


(1)求证:AE=![]() NE+ME;
NE+ME;
(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.猜想CH与FH存在的数量关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
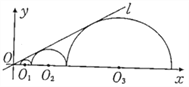
【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On均与直线l相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当直线l与x轴所成锐角为30![]() 时,且r1=1时,r2017=_______.
时,且r1=1时,r2017=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部数学专著,它的出现标志中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)( )
A.3B.5C.4.2D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题情境]
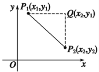
我们知道数轴上的两点A、B的距离|AB|=|xA-xB|,那么如果已知平面上两点P1(x1,y1),P2(x2,y2),如何求P1,P2的距离d(P1P2)呢?
下面我们就来研究这个问题.
问题 一般地,已知平面上两点P1(x1,y1),P2(x2,y2),如何求点P1和P2的距离?
答: 当x1≠x2,y1=y2时,|P1P2|=|x2-x1|;
当x1=x2,y1≠y2时,|P1P2|=|y2-y1|;
当x1≠x2,y1≠y2时,如图,
在Rt△P1QP2中,由勾股定理知,
|P1P2|2=|P1Q|2+|QP2|2,所以d(P1,P2)=|P1P2|=![]() .
.
归纳:两点P1(x1,y1),P2(x2,y2)间的距离公式d(P1,P2)=|P1P2|=![]() .
.
解决问题:
(1)已知A(2,-4),B(-2,3),求d(A,B)
(2)已知点A(1,2),B(3,4),C(5,0),求证:△ABC是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com