
ЁОЬтФПЁПОРњвпЧщИДбЇКѓЃЌбЇаЃПЊеЙСЫЖржжаЮЪНЕФЗРвпжЊЪЖНВзљЃЌВЂОйааСЫШЋдБВЮМгЕФЁАЗРвпЁБжЊЪЖОКШќЃЌЪдОэЬтФПЙВ10ЬтЃЌУПЬт10ЗжЃЎЯжЗжБ№ДгЦпФъМЖ1,2,3АржаИїЫцЛњГщШЁ10УћЭЌбЇЕФГЩМЈЃЈЕЅЮЛЃКЗжЃЉЃЎ
ЪеМЏећРэЪ§ОнШчЯТЃК
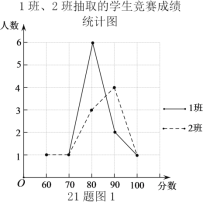
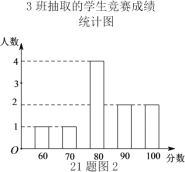
ЗжЮіЪ§ОнЃК
ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | |
1Ар | 83 |
| 80 |
2Ар | 83 |
|
|
3Ар |
| 80 | 80 |
ИљОнвдЩЯаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыжБНгаДГіБэИёжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉБШНЯетШ§зщбљБОЪ§ОнЕФЦНОљЪ§ЁЂжаЮЛЪ§КЭжкЪ§ЃЌФуШЯЮЊФФИіАрЕФГЩМЈБШНЯКУЃПЧыЫЕУїРэгЩЃЈвЛЬѕРэгЩМДПЩЃЉЃЛ
ЃЈ3ЃЉЮЊСЫШУбЇЩњжиЪгАВШЋжЊЪЖЕФбЇЯАЃЌбЇаЃНЋИјОКШќГЩМЈТњЗжЕФЭЌбЇАфЗЂНБзДЃЌИУаЃЦпФъМЖбЇЩњЙВ120ШЫЃЌЪдЙРМЦашвЊзМБИЖрЩйеХНБзДЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ,
,![]() ,
,![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЮвШЯЮЊЦпФъМЖ2АрЕФГЩМЈБШНЯКУЃЌЫцЛњГщШЁЕФбљБОжаЃЌШ§ИіАрбљБОГЩМЈЕФЦНОљЪ§ЖМЮЊ83ЃЌ 2АрГЩМЈЕФжаЮЛЪ§ЮЊ85ЃЌДѓгк1АрКЭ3АрГЩМЈЕФжаЮЛЪ§80ЃЛ2АрГЩМЈЕФжкЪ§90Дѓгк1АрКЭ3АрГЩМЈЕФжкЪ§80ЃЛЃЈ3ЃЉЙРМЦашвЊзМБИЕФНБзДЪЧ16еХЃЎ
ЃЛЃЈ2ЃЉЮвШЯЮЊЦпФъМЖ2АрЕФГЩМЈБШНЯКУЃЌЫцЛњГщШЁЕФбљБОжаЃЌШ§ИіАрбљБОГЩМЈЕФЦНОљЪ§ЖМЮЊ83ЃЌ 2АрГЩМЈЕФжаЮЛЪ§ЮЊ85ЃЌДѓгк1АрКЭ3АрГЩМЈЕФжаЮЛЪ§80ЃЛ2АрГЩМЈЕФжкЪ§90Дѓгк1АрКЭ3АрГЩМЈЕФжкЪ§80ЃЛЃЈ3ЃЉЙРМЦашвЊзМБИЕФНБзДЪЧ16еХЃЎ
ЁОНтЮіЁП
(1)ИљОнЦНОљЪ§ЁЂжкЪ§ЁЂжаЮЛЪ§ЗжБ№ЧѓНтМДПЩЕУЕНД№АИЃЛ
(2)ИљОнШ§ИіАрЦНОљЗжЖМЪЧ83ЗжЃЌдйЗжЮіжаЮЛЪ§вдМАжкЪ§ЃЌМДПЩЕУЕНД№АИЃЛ
(3)ИљОнЕїВщШЫЪ§ЕФТњЗжЧщПіЙРЫузмШЫЪ§ЕФТњЗжЧщПіЃЌМДПЩЕУЕНД№АИЃЛ
НтЃКЃЈ1ЃЉДгЬѕаЮЭГМЦЭМЕУЕНЃК![]() ЃЌ
ЃЌ
ИљОнжаЮЛЪ§ЕФЖЈвхЃЌ1ЁЂ2АрЕїВщШЫЪ§ЮЊ10ШЫЃЌМДЗжЪ§ДгаЁЕНДѓХХађЃЌЕк5Ек6УћЭЌбЇЕФЦНОљГЩМЈМДЪЧжаЮЛЪ§ЃЌ
ДгелЯпЭМЕУЕН1Ар70ЗжвЛУћЭЌбЇЃЌ80Зж6УћЭЌбЇЃЌ
ЙЪ![]() ЃЌ
ЃЌ
ДгелЯпЭМЕУЕН2Ар60ЗжвЛУћЭЌбЇЃЌ70ЗжвЛУћЭЌбЇЃЌ80Зж3УћЭЌбЇЃЌ90ЗжЫФУћЭЌбЇЃЌ
ЙЪ![]() ЃЌ
ЃЌ
2Ар90ЗжШЫЪ§зюЖрЃЌЙЪжкЪ§c=90ЃЌ
ЙЪЃК![]() ,
,![]() ,
,![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЮвШЯЮЊЦпФъМЖ2АрЕФГЩМЈБШНЯКУЃЌРэгЩШчЯТЃК
ЫцЛњГщШЁЕФбљБОжаЃЌШ§ИіАрбљБОГЩМЈЕФЦНОљЪ§ЖМЮЊ83ЃЌ 2АрГЩМЈЕФжаЮЛЪ§ЮЊ85ЃЌДѓгк1АрКЭ3АрГЩМЈЕФжаЮЛЪ§80ЃЛ
2АрГЩМЈЕФжкЪ§90Дѓгк1АрКЭ3АрГЩМЈЕФжкЪ§80ЃЌ
вђДЫЮвШЯЮЊ2АрГЩМЈНЯКУ ЃЎ
ЃЈ3ЃЉвђЮЊЫљГщШЁЕФбљБОжаЃЌбљБОзмСПЪЧ30ЃЌЖјЦфжаТњЗжШЫЪ§ЪЧ1+1+2=4ЃЎ
ЫљвдЃЌ![]() ЃЎ
ЃЎ
Д№ЃКЙРМЦашвЊзМБИЕФНБзДЪЧ16еХЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
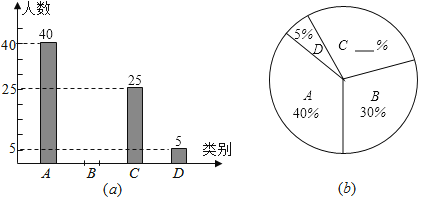
ЁОЬтФПЁПЮЊСЫСЫНтФГЧј2018ФъГѕжаБЯвЕЩњБЯвЕКѓЕФШЅЯђЃЌФГЧјНЬг§ВПУХЖдВПЗжГѕШ§бЇЩњНјааСЫГщбљЕїВщЃЌОЭГѕШ§бЇЩњЕФЫФжжШЅЯђЃЈAЃЌЖСЦеЭЈИпжаЃЛBЃЌЖСжАвЕИпжаЃЛCЃЌжБНгНјШыЩчЛсОЭвЕЃЛDЃЌЦфЫќЃЉНјааЪ§ОнЭГМЦЃЌВЂЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЈaЃЉЁЂЃЈbЃЉЃЎЧыЮЪЃК
ЃЈ1ЃЉДЫДЮЙВЕїВщСЫЖрЩйУћГѕжаБЯвЕЩњЃП
ЃЈ2ЃЉНЋСНЗљЭГМЦЭМжаВЛЭъећЕФВПЗжВЙГфЭъећЃЛ
ЃЈ3ЃЉШєФГЧј2018ФъГѕШ§БЯвЕЩњЙВга3500ШЫЃЌЧыЙРМЦ2019ФъГѕШ§БЯвЕЩњжаЖСЦеЭЈИпжаЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
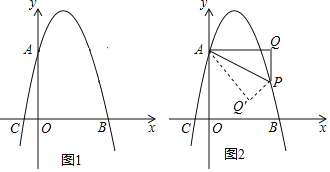
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯпyЃНЉx2+bx+cНЛyжсгкЕуA(0ЃЌ4)ЃЌНЛxжсгкЕуB(4ЃЌ0)ЃЌЕуPЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЪдЙ§ЕуPзїxжсЕФДЙЯп1ЃЌдйЙ§ЕуAзї1ЕФДЙЯпЃЌДЙзуЮЊQЃЌСЌНгAPЃЎ
(1)ЧѓХзЮяЯпЕФКЏЪ§БэДяЪНКЭЕуCЕФзјБъЃЛ
(2)ШєЁїAQPЁзЁїAOCЃЌЧѓЕуPЕФКсзјБъЃЛ
(3)ШчЭМ2ЃЌЕБЕуPЮЛгкХзЮяЯпЕФЖдГЦжсЕФгвВрЪБЃЌШєНЋЁїAPQбиAPЖделЃЌЕуQЕФЖдгІЕуЮЊЕуQЁфЃЌЧыжБНгаДГіЕБЕуQЁфТфдкзјБъжсЩЯЪБЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌEЪЧОиаЮABCDЕФБпBCЩЯвЛЕуЃЌEFЁЭAEЃЌЗжБ№НЛACЃЌCDгкЕуMЃЌFЃЌBGЁЭACЃЌДЙзуЮЊGЃЌBGНЛAEгкЕуHЃЎ
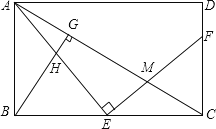
ЃЈ1ЃЉЧѓжЄЃКЁїABEЁзЁїECFЃЛ
ЃЈ2ЃЉевГігыЁїABHЯрЫЦЕФШ§НЧаЮЃЌВЂжЄУїЃЛ
ЃЈ3ЃЉШєEЪЧBCжаЕуЃЌBC=2ABЃЌAB=4ЃЌЧѓEMЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯп![]() гыxжсЯрНЛгкAЁЂBСНЕу(ЕуAдкЕуBЕФзѓВр)ЃЌгыyжсНЛгкЕуCЃЎ
гыxжсЯрНЛгкAЁЂBСНЕу(ЕуAдкЕуBЕФзѓВр)ЃЌгыyжсНЛгкЕуCЃЎ
(1)ЧѓжБЯпBCЕФНтЮіЪНЃЎ
(2)ЕуPЪЧЯпЖЮBCЯТЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЎ
ЂйЧѓЫФБпаЮPBACУцЛ§ЕФзюДѓжЕЃЌВЂЧѓЫФБпаЮPBACУцЛ§ЕФзюДѓЪБPЕуЕФзјБъЃЛ
ЂкШчЙћдкxжсЩЯДцдкЕуQЃЌЪЙЕУвдЕуBЁЂCЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎЧѓЕуQЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮABCDжаЃЌЕуEЪЧБпBCЩЯвЛЕуЃЌСЌНгAEЃЌЙ§ЕуEзїEMЁЭAEЃЌНЛЖдНЧЯпACгкЕуMЃЌЙ§ЕуMзїMNЁЭABЃЌДЙзуЮЊNЃЌСЌНгNEЃЎ


ЃЈ1ЃЉЧѓжЄЃКAE=![]() NE+MEЃЛ
NE+MEЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌбгГЄEMжСЕуFЃЌЪЙEF=EAЃЌСЌНгAFЃЌЙ§ЕуFзїFHЁЭDCЃЌДЙзуЮЊHЃЎВТЯыCHгыFHДцдкЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЁЯAЃН30ЁуЃЌНЋЁїABCШЦCЕуАДФцЪБеыЗНЯђа§зЊ![]() НЧ(0ЁуЃМ
НЧ(0ЁуЃМ![]() ЃМ90Ёу)ЕУЕНЁїDECЃЌЩшCDНЛABгкЕуFЃЌСЌНгADЃЌЕБа§зЊНЧ
ЃМ90Ёу)ЕУЕНЁїDECЃЌЩшCDНЛABгкЕуFЃЌСЌНгADЃЌЕБа§зЊНЧ![]() ЖШЪ§ЮЊ________ЃЌЁїADFЪЧЕШбќШ§НЧаЮЃЎ
ЖШЪ§ЮЊ________ЃЌЁїADFЪЧЕШбќШ§НЧаЮЃЎ
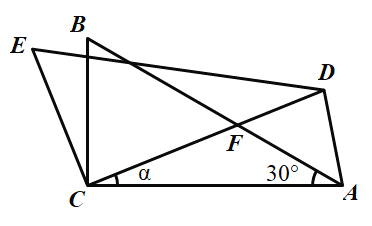
A.20ЁуB.40ЁуC.10ЁуD.20ЁуЛђ40Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
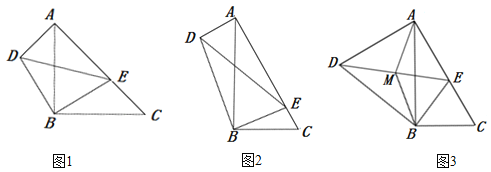
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯж
ШчЭМ1ЃЌдкRtЁїABCКЭRtЁїDBEжаЃЌЁЯABC=ЁЯDBE=90ЁуЃЌЁЯACB=ЁЯBED=45ЁуЃЌЕуEЪЧЯпЖЮACЩЯвЛЖЏЕуЃЌСЌНгDEЃЎ
ЬюПеЃКЂйдђ![]() ЕФжЕЮЊ______ЃЛЂкЁЯEADЕФЖШЪ§ЮЊ_______ЃЎ
ЕФжЕЮЊ______ЃЛЂкЁЯEADЕФЖШЪ§ЮЊ_______ЃЎ
ЃЈ2ЃЉРрБШЬНОП
ШчЭМ2ЃЌдкRtЁїABCКЭRtЁїDBEжаЃЌЁЯABC=ЁЯDBE=90ЁуЃЌЁЯACB=ЁЯBED=60ЁуЃЌЕуEЪЧЯпЖЮACЩЯвЛЖЏЕуЃЌСЌНгDEЃЎЧыЧѓГі![]() ЕФжЕМАЁЯEADЕФЖШЪ§ЃЛ
ЕФжЕМАЁЯEADЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЭиеЙбгЩь
ШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШЁЯпЖЮDEЕФжаЕуMЃЌСЌНгAMЁЂBMЃЌШєBC=4ЃЌдђЕБЁїABMЪЧжБНЧШ§НЧаЮЪБЃЌЧѓЯпЖЮADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
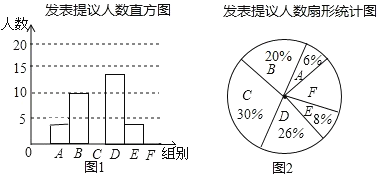
ЁОЬтФПЁПСНЛсЦкМфЃЌМЧепЫцЛњГщШЁВЮЛсЕФВПЗжДњБэЃЌЖдЫћУЧФГЬьЗЂбдЕФДЮЪ§НјааСЫЭГМЦЃЌЦфНсЙћШчБэЃЌВЂЛцжЦСЫШчЭМЫљЪОЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыНсКЯЭМжаЯрЙиЪ§ОнЛиД№ЯТСаЮЪЬтЃК
ЗЂбдДЮЪ§n | |
A | 0ЁмnЃМ3 |
B | 3ЁмnЃМ6 |
C | 6ЁмnЃМ9 |
D | 9ЁмnЃМ12 |
E | 12ЁмnЃМ15 |
F | 15ЁмnЃМ18 |
ЃЈ1ЃЉЧѓЕУбљБОШнСПЮЊЁЁЁЁЃЌВЂВЙШЋжБЗНЭМЃЛ
ЃЈ2ЃЉвбжЊAзщЗЂБэЬсвщЕФДњБэжаЧЁга1ЮЛХЎЪПЃЌEзщЗЂБэЬсвщЕФДњБэжажЛга2ЮЛФаЪПЃЌЯжДгAзщгыEзщжаЗжБ№ГщвЛЮЛДњБэаДБЈИцЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓЫљГщЕФСНЮЛДњБэЧЁКУЖМЪЧФаЪПЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com