
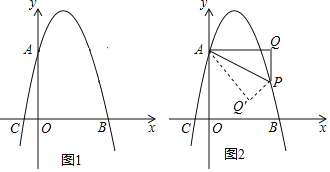
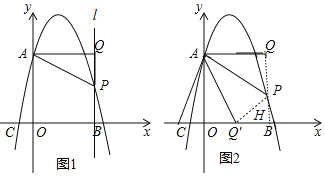
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.
(1)求抛物线的函数表达式和点C的坐标;
(2)若△AQP∽△AOC,求点P的横坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.
【答案】(1)y=﹣x2+3x+4;(﹣1,0);(2)P的横坐标为![]() 或
或![]() .(3)点P的坐标为(4,0)或(5,﹣6)或(2,6).
.(3)点P的坐标为(4,0)或(5,﹣6)或(2,6).
【解析】
(1)利用待定系数法求抛物线解析式,然后利用抛物线解析式得到一元二次方程,通过解一元二次方程得到C点坐标;
(2)利用△AQP∽△AOC得到AQ=4PQ,设P(m,﹣m2+3m+4),所以m=4|4﹣(﹣m2+3m+4|,然后解方程4(m2﹣3m)=m和方程4(m2﹣3m)=﹣m得P点坐标;
(3)设P(m,﹣m2+3m+4)(m>![]() ),当点Q′落在x轴上,延长QP交x轴于H,如图2,则PQ=m2﹣3m,证明Rt△AOQ′∽Rt△Q′HP,利用相似比得到Q′B=4m﹣12,则OQ′=12﹣3m,在Rt△AOQ′中,利用勾股定理得到方程42+(12﹣3m)2=m2,然后解方程求出m得到此时P点坐标;当点Q′落在y轴上,易得点A、Q′、P、Q所组成的四边形为正方形,利用PQ=PQ′得到|m2﹣3m|=m,然后解方程m2﹣3m=m和方程m2﹣3m=﹣m得此时P点坐标.
),当点Q′落在x轴上,延长QP交x轴于H,如图2,则PQ=m2﹣3m,证明Rt△AOQ′∽Rt△Q′HP,利用相似比得到Q′B=4m﹣12,则OQ′=12﹣3m,在Rt△AOQ′中,利用勾股定理得到方程42+(12﹣3m)2=m2,然后解方程求出m得到此时P点坐标;当点Q′落在y轴上,易得点A、Q′、P、Q所组成的四边形为正方形,利用PQ=PQ′得到|m2﹣3m|=m,然后解方程m2﹣3m=m和方程m2﹣3m=﹣m得此时P点坐标.
解:(1)把A(0,4),B(4,0)分别代入y=﹣x2+bx+c得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+3x+4,
当y=0时,﹣x2+3x+4=0,解得x1=﹣1,x2=4,
∴C(﹣1,0);
故答案为y=﹣x2+3x+4;(﹣1,0);
(2)∵△AQP∽△AOC,
∴![]() ,
,
∴![]() ,即AQ=4PQ,
,即AQ=4PQ,
设P(m,﹣m2+3m+4),
∴m=4|4﹣(﹣m2+3m+4|,即4|m2﹣3m|=m,
解方程4(m2﹣3m)=m得m1=0(舍去),m2=![]() ,此时P点横坐标为
,此时P点横坐标为![]() ;
;
解方程4(m2﹣3m)=﹣m得m1=0(舍去),m2=![]() ,此时P点坐标为
,此时P点坐标为![]() ;
;
综上所述,点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)设![]() ,
,
当点Q′落在x轴上,延长QP交x轴于H,如图2,
则PQ=4﹣(﹣m2+3m+4)=m2﹣3m,
∵△APQ沿AP对折,点Q的对应点为点Q',
∴∠AQ′P=∠AQP=90°,AQ′=AQ=m,PQ′=PQ=m2﹣3m,
∵∠AQ′O=∠Q′PH,
∴Rt△AOQ′∽Rt△Q′HP,
∴![]() ,即
,即![]() ,解得Q′H=4m﹣12,
,解得Q′H=4m﹣12,
∴OQ′=m﹣(4m﹣12)=12﹣3m,
在Rt△AOQ′中,42+(12﹣3m)2=m2,
整理得m2﹣9m+20=0,解得m1=4,m2=5,此时P点坐标为(4,0)或(5,﹣6);
当点Q′落在y轴上,则点A、Q′、P、Q所组成的四边形为正方形,
∴PQ=AQ′,
即|m2﹣3m|=m,
解方程m2﹣3m=m得m1=0(舍去),m2=4,此时P点坐标为(4,0);
解方程m2﹣3m=﹣m得m1=0(舍去),m2=2,此时P点坐标为(2,6),
综上所述,点P的坐标为(4,0)或(5,﹣6)或(2,6)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随杋抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
学生最喜爱的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | |
中国诗词大会 |
| 40% |
出彩中国人 | 10 | 20% |
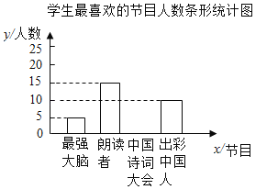
根据以上信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)补全上面的条形统计图;
(3)若该校共有学生![]() 名,估计该校学生最喜爱《朗读者》节目的人数.
名,估计该校学生最喜爱《朗读者》节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全国预防“新冠肺炎”时期,某厂接受了生产一批高质量医用口罩的任务.要求8天之内(含8天)生产![]() 型和
型和![]() 型两种型号的口罩共5万只,其中
型两种型号的口罩共5万只,其中![]() 型口罩不得少于1.8万只.该厂的生产能力是:每天只能生产一种型号的口罩,若生产
型口罩不得少于1.8万只.该厂的生产能力是:每天只能生产一种型号的口罩,若生产![]() 型口罩每天能生产0.6万只,若生产
型口罩每天能生产0.6万只,若生产![]() 型口罩每天能生产0.8万只.已知生产6只
型口罩每天能生产0.8万只.已知生产6只![]() 型和10只
型和10只![]() 型口罩一共获利6元,生产4只
型口罩一共获利6元,生产4只![]() 型和5只
型和5只![]() 型口罩一共获利3.5元
型口罩一共获利3.5元
(1)生产一只![]() 型口罩和
型口罩和![]() 型口罩分别获利多少钱?
型口罩分别获利多少钱?
(2)若生产![]() 型口罩
型口罩![]() 万只,该厂这次生产口罩的总利润为
万只,该厂这次生产口罩的总利润为![]() 万元,请求出
万元,请求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在完成任务的前提下,如何安排生产![]() 型和
型和![]() 型口罩的只数,使获得的总利润最大?最大利润是多少?
型口罩的只数,使获得的总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣mx+n.
(1)当m=2时,
①求抛物线的对称轴,并用含n的式子表示顶点的纵坐标;
②若点A(﹣2,y1),B(x2,y2)都在抛物线上,且y2>y1,则x2的取值范围是 ;
(2)已知点P(﹣1,2),将点P向右平移4个单位长度,得到点Q.当n=3时,若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师准备了四张背面都一样的卡片A、B、C、D,每张卡片的正面标有字母a、b、c表示三条线段(如下图).把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.

⑴ 李老师随机抽取一张卡片,抽到卡片B的概率等于 ;
⑵ 求李老师抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
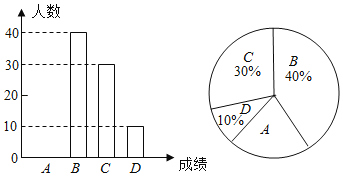
【题目】我校为了了解九年级学生身体素质测试情况,随机抽取了本校九年级部分学生的身体素质测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如图不完整的统计图,请你结合图表所给信息解答下列问题:
(1)请在答题卡上直接将条形统计图补充完整;
(2)扇形统计图中“B”部分所对应的圆心角的度数是 °;
(3)若我校九年级共有1500名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经历疫情复学后,学校开展了多种形式的防疫知识讲座,并举行了全员参加的“防疫”知识竞赛,试卷题目共10题,每题10分.现分别从七年级1,2,3班中各随机抽取10名同学的成绩(单位:分).
收集整理数据如下:
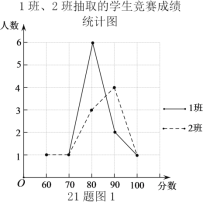
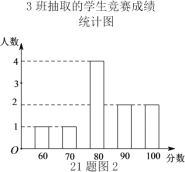
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 |
| 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由(一条理由即可);
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级学生共120人,试估计需要准备多少张奖状?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com