
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,
,![]() ,求菱形
,求菱形![]() 的面积.
的面积.
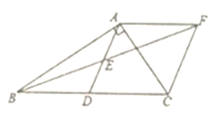
【答案】(1)证明见解析;(2)96.
【解析】
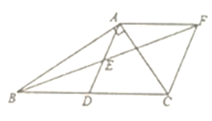
(1)先证明△AEF≌△DEB,可得AF=DB=DC,进而证明四边形ADCF是平行四边形,然后由直角三角形斜边中线的性质得AD=CD,即可证明四边形ADCF是菱形;
(2)求出菱形ADCF的面积=直角三角形ABC的面积,然后解答即可.
(1)证明:∵E是AD的中点,
∴AE=DE
∵AF∥BC,
∴∠AFE=∠DBE,
∵在△AEF和△DEB中,∠AFE=∠DBE,∠AEF=∠DEB,AE=DE,
∴△AEF≌△DEB(AAS),
∴AF=DB=DC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=CD=![]() BC,
BC,
∴平行四边形ADCF是菱形;
(2)解:设AF到CD的距离为h,
∵AF∥BC,AF=BD=CD,∠BAC=90°,
∴S菱形ADCF=CD·h=![]() BC·h=S△ABC=
BC·h=S△ABC=![]() AB·AC=
AB·AC=![]() ×12×16=96.
×12×16=96.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
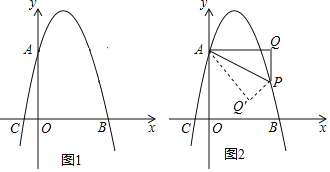
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.
(1)求抛物线的函数表达式和点C的坐标;
(2)若△AQP∽△AOC,求点P的横坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
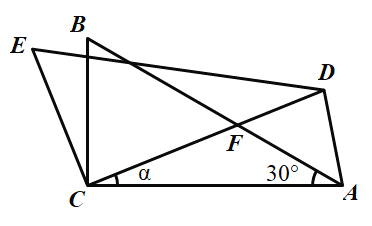
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转![]() 角(0°<
角(0°<![]() <90°)得到△DEC,设CD交AB于点F,连接AD,当旋转角
<90°)得到△DEC,设CD交AB于点F,连接AD,当旋转角![]() 度数为________,△ADF是等腰三角形.
度数为________,△ADF是等腰三角形.
A.20°B.40°C.10°D.20°或40°
查看答案和解析>>
科目:初中数学 来源: 题型:
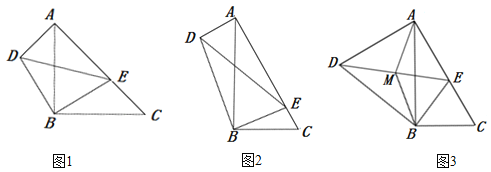
【题目】(1)问题发现
如图1,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=45°,点E是线段AC上一动点,连接DE.
填空:①则![]() 的值为______;②∠EAD的度数为_______.
的值为______;②∠EAD的度数为_______.
(2)类比探究
如图2,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=60°,点E是线段AC上一动点,连接DE.请求出![]() 的值及∠EAD的度数;
的值及∠EAD的度数;
(3)拓展延伸
如图3,在(2)的条件下,取线段DE的中点M,连接AM、BM,若BC=4,则当△ABM是直角三角形时,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
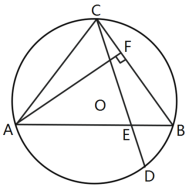
【题目】如图,△ABC内接于⊙O,AC=BC,弦CD与AB交于E,AB=CD,过A作AF⊥BC于F.
(1)判断AC与BD的位置关系,并说明理由;
(2)求证:AC=2CF+BD;
(3)若S△CFA=S△CBD,求tan∠BDC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
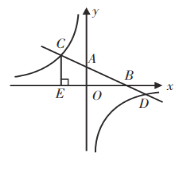
【题目】已知:如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() ,
,![]() 轴交于点
轴交于点![]() ,
,![]() ,与反比例函数的图象分别交于点
,与反比例函数的图象分别交于点![]() ,
,![]() ,
, ![]() 轴于点
轴于点![]() ,
, ![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)求反比例函数的解析式;
(3)连接![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,但须保留作图痕迹).
(2)已知内角度数的两个三角形如图2,图3所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
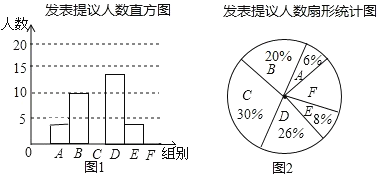
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
(1)求得样本容量为 ,并补全直方图;
(2)已知A组发表提议的代表中恰有1位女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种高档蔬菜“莼菜”,其进价为16元/kg.经市场调查发现:该商品的日销售量y(kg)是售价x(元/kg)的一次函数,其售价、日销售量对应值如表:
售价 | 20 | 30 | 40 |
日销售量 | 80 | 60 | 40 |
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围);
的函数解析式(不要求写出自变量的取值范围);
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)由于产量日渐减少,该商品进价提高了![]() 元/
元/![]() ,物价部门规定该商品售价不得超过36元/
,物价部门规定该商品售价不得超过36元/![]() ,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求
,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com