
【题目】如图,△ABC内接于⊙O,AC=BC,弦CD与AB交于E,AB=CD,过A作AF⊥BC于F.
(1)判断AC与BD的位置关系,并说明理由;
(2)求证:AC=2CF+BD;
(3)若S△CFA=S△CBD,求tan∠BDC的值.
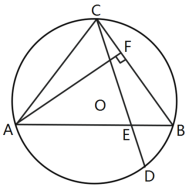

【答案】(1)AC∥BD,见解析;(2)见解析;(3)![]()
【解析】
(1)连接BD和AD,根据圆心角、弦和圆心角的关系,即可判断.
(2)在BC上找一点M,使得BM=BD,根据圆周角定理判断出AD和AC的关系,然后根据三角形全等判断AD和AM的关系,从而得出AM=AC,再根据三线合一,判断出CF=FM,从而得出结论.
(3)分别过点B和点C 向AC和DB作垂线,根据平行线间的距离相等,得出BN=CG,再根据两三角形面积相等,即可判断出BD和CF的关系,再结合第(2)问,可以得出F点是BC的三等分点,然后设出CF的边长为m,用m将AF和BF表示出来,根据圆周角定理及其推论得出∠CDB=∠ABF,然后代入即可计算.
解:(1)AC∥BD.
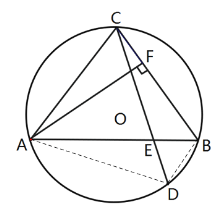
连接AD,BD,
∵AB=CD,
∴∠CAD=∠CBD,
又∵∠DAB=∠BCD,
∴∠CAB=∠ACD,
∵∠CAB=∠CDB
∴∠ACD=∠CDB
∴AC∥BD.
(2)在BC上找一点M,使BM=BD,
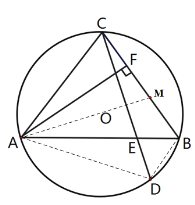
连接AM,AD
∵AC∥BD,
∴∠ACD=∠CDB,
∴AD=BC,
又∵AC=BC,
∴AD=AC,
∴∠ABD=∠ABM,
∵BA=BA
∴△AMB≌ADB,
∴AM=AD,
∴AM=AC
又∵AF⊥BC,
∴CF=FM
∵BC=CF+FM+MB=2CF+MB=2CF+BD
∵AC=BC,
∴AC=2CF+BD.
过B点向AC做垂线,垂足为N,
连接DB并延长DB,过C点向DB作垂线,与DB延长线交于点G,由图可知CG即为
△CBD的高.
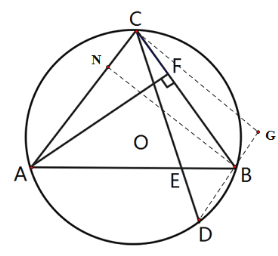
∵AC=BC,
∴BD=AF,
∵AC∥DB,
∴BN=CG,
∴BN=CG,
AF=CG,
![]()
![]()
又∵S△CFA=S△CBD,
∴BD=CF,
∵BC=2CF+BD.
∴BC=3CF,
设CF为m,则AC=3m,BF=BC-CF=2m,
![]()
∵AC=BC,
∴∠BDC=∠ABF
![]()


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】数学课上,李老师准备了四张背面都一样的卡片A、B、C、D,每张卡片的正面标有字母a、b、c表示三条线段(如下图).把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.

⑴ 李老师随机抽取一张卡片,抽到卡片B的概率等于 ;
⑵ 求李老师抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
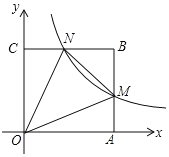
【题目】如图,在平面直角坐标系中,边长为1的正方形OABC的顶点O与原点重合,顶点A,C分别在x轴、y轴上,反比例函数y=![]() (k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,连接OM、ON、MN.若∠MON=45°,则k的值为_____.
(k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,连接OM、ON、MN.若∠MON=45°,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春,受疫情影响,同学们进行了3个多月的网课迎来了复学,为了解九年级学生网课期间学习情况,学校在复学后进行了复学测试,小虎同学在九年级随机抽取了一部分学生的复学测试数学成绩为样本,分为A(100~90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
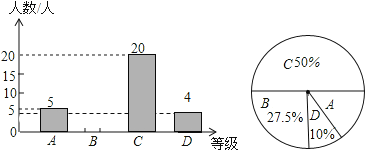
其中C组的期末数学成绩如下:
61 | 63 | 65 | 66 | 66 | 67 | 69 | 70 | 72 | 73 |
75 | 75 | 76 | 77 | 77 | 77 | 78 | 78 | 79 | 79 |
(1)请补全条形统计图;
(2)扇形统计图中A组所占的圆心角的度数为______,C组的复学测试数学成绩的中位数是______,众数是_______;
(3)这个学校九年级共有学生400人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生复学测试数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
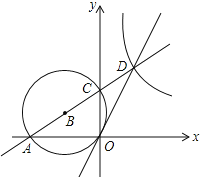
【题目】如图,在平面直角坐标系中,半径为![]() 的⊙B经过原点O,且与x,y轴分交于点A,C,点C的坐标为(0,2),AC的延长线与⊙B的切线OD交于点D,则经过D点的反比例函数的解析式为_______.
的⊙B经过原点O,且与x,y轴分交于点A,C,点C的坐标为(0,2),AC的延长线与⊙B的切线OD交于点D,则经过D点的反比例函数的解析式为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣4x+3和一次函数y=﹣x+1,我们把y=t(x2﹣4x+3)+(1﹣t)(﹣x+1)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n),请完成下列任务:
(尝试)
⑴判断点A是否在抛物线E上;
⑵求n的值.
(发现)通过(1)和(2)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,请你求出定点的坐标.
(应用)二次函数y=﹣3x2+8x﹣5是二次函数y=x2﹣4x+3和一次函数y=﹣x+1的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广宇、承义两名同学分别进行5次射击训练,训练成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
广宇 | 9 | 8 | 7 | 7 | 9 |
承义 | 6 | 8 | 10 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A.广宇训练成绩的平均数大于承义训练成绩平均数
B.广宇训练成绩的中位数与承义训练成绩中位数不同
C.广宇训练成绩的众数与承义训练成绩众数相同
D.广宇训练成绩比承义训练成绩更加稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com