
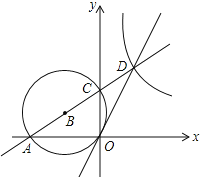
【题目】如图,在平面直角坐标系中,半径为![]() 的⊙B经过原点O,且与x,y轴分交于点A,C,点C的坐标为(0,2),AC的延长线与⊙B的切线OD交于点D,则经过D点的反比例函数的解析式为_______.
的⊙B经过原点O,且与x,y轴分交于点A,C,点C的坐标为(0,2),AC的延长线与⊙B的切线OD交于点D,则经过D点的反比例函数的解析式为_______.
【答案】![]()
【解析】
连接OB,分别求出点A、B的坐标,利用待定系数法分别求出AC和OB的解析式,结合OD是圆B的切线,可得到OD的直线表达式,然后联立方程组,求出点D的坐标,再根据点D的坐标求得反比例函数的表达式.
如图,连接OB,
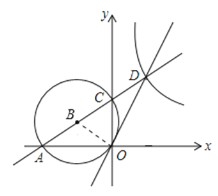
∵C(0,2),BC=![]()
∴OC=2,AC=2![]()
∵OC⊥AO,
∴![]()
∴A(-4,0)
设直线AC的解析式为:y=kx+b
把A(-4,0),C(0,2)代入得:![]()
解得:![]()
∴直线AC的表达式为:![]()
∵点B为AC的中点,
∴B(-2,1)
设OB的表达式为:y=mx,则m=-![]() ,
,
∴y=-![]() x,
x,
∵OB⊥OD,
∴直线OD的解析式为:y=2x
联立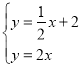
解得,![]() ,即点D(
,即点D(![]() ,
,![]() )
)
设经过D点的反比例函数的解析式为![]() ,则k=
,则k=![]() ×
×![]() =
=![]()
∴![]() .
.
故答案为:![]()
![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、CEFG都是正方形,E在CD上且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,下列四个结论:
① BE⊥GD; ② OH=![]() BG; ③ ∠AHD=45°; ④ GD=
BG; ③ ∠AHD=45°; ④ GD=![]() AM.
AM.
其中正确的结论个数有

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在疫情期间,某地推出线上名师公益大课堂,为广大师生、其他社会人士提供线上专业知识学习、心理健康疏导.参与学习第一批公益课的人数达到2万人,因该公益课社会反响良好,参与学习第三批公益课的人数达到2.42万人.参与学习第二批、第三批公益课的人数的增长率相同.
(1)求这个增长率;
(2)据大数据统计,参与学习第三批公益课的人数中,师生人数在参与学习第二批公益课的师生人数的基础上增加了80%;但因为已经部分复工,其他社会人士的人数在参与学习第二批公益课的其他社会人士人数的基础上减少了60%.求参与学习第三批公益课的师生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A (1,3),这两条直线分别与x轴交于B,C两点.
交于点A (1,3),这两条直线分别与x轴交于B,C两点.
(1)求k的值;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
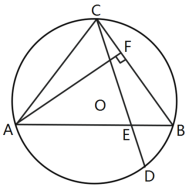
【题目】如图,△ABC内接于⊙O,AC=BC,弦CD与AB交于E,AB=CD,过A作AF⊥BC于F.
(1)判断AC与BD的位置关系,并说明理由;
(2)求证:AC=2CF+BD;
(3)若S△CFA=S△CBD,求tan∠BDC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
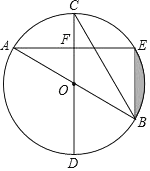
【题目】如图,已知AB,CD为⊙O的直径,过点A作弦AE垂直于直径CD于F,点B恰好为弧DE的中点,连接BC,BE.
(1)求证:AE=BC;
(2)若AE=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在(2)的条件下,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
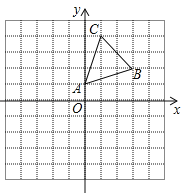
【题目】(2016甘肃省白银市)如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需要采购A、B两种笔记本,A种笔记本的单价高出B种笔记本的单价10元,并且花费300元购买A种笔记本和花费100元购买B种笔记本的数量相等.
(1)求A种笔记本和B种笔记本的单价各是多少元;
(2)该公司准备采购A、B两种笔记本共80本,若A种笔记本的数量不少于60本,并且采购A、B两种笔记本的总费用不高于1100元,那么该公司有 种购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com