
【题目】如图,四边形ABCD、CEFG都是正方形,E在CD上且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,下列四个结论:
① BE⊥GD; ② OH=![]() BG; ③ ∠AHD=45°; ④ GD=
BG; ③ ∠AHD=45°; ④ GD=![]() AM.
AM.
其中正确的结论个数有

A.1个B.2个C.3个D.4个
【答案】D
【解析】
①由已知条件可证得△BEC≌△DGC,∠EBC=∠CDG,因为∠BDC+∠DBH+∠EBC=90°,所以∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;
②由①可以证明△BHD≌△BHG,就可以得到DH=GH,得出OH是△BGD的中位线,从而得出结论.
③若以BD为直径作圆,那么此圆必经过A、B、C、H、D五点,根据圆周角定理即可得到∠AHD=45°,所以②的结论也是正确的.
④此题要通过相似三角形来解;由②的五点共圆,可得∠BAH=∠BDH,而∠ABD=∠DBG=45°,由此可判定△ABM∽△DBG,根据相似三角形的比例线段即可得到AM、DG的比例关系;
解:①正确,证明如下:
∵BC=DC,CE=CG,∠BCE=∠DCG=90°,
∴△BEC≌△DGC,
∴∠EBC=∠CDG,
∵∠BDC+∠DBH+∠EBC=90°,
∴∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;
②∵BE平分∠DBC,
∴∠DBH=∠GBH.
∵BE⊥GD,
∴∠BHD=∠BHG=90°.
在△BHD和△BHG中
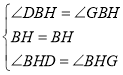 ,
,
∴△BHD≌△BHG(ASA),
∴DH=GH.
∵O是BD中点,
∴DO=BO.
∴OH是△BDG的中位线,
∴OH=![]() BG,故②正确;
BG,故②正确;
③由于∠BAD、∠BCD、∠BHD都是直角,因此A、B、C、D、H五点都在以BD为直径的圆上;
由圆周角定理知:∠DHA=∠ABD=45°,故③正确;
④由②知:A、B、C、D、H五点共圆,则∠BAH=∠BDH;
又∵∠ABD=∠DBG=45°,
∴△ABM∽△DBG,得AM:DG=AB:BD=1:![]() ,即DG=
,即DG=![]() AM;
AM;
故④正确;
∴正确的个数有4个.
故选:D.


科目:初中数学 来源: 题型:
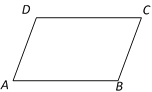
【题目】已知:在平行四边形ABCD中,AB︰BC=3︰2.
(1)根据条件画图:作∠BCD的平分线,交边AB于点E,取线段BE的中点F,连接DF交CE于点G.
(2)设![]() ,那么向量
,那么向量![]() =______.(用向量
=______.(用向量![]() 、
、![]() 表示),并在图中画出向量
表示),并在图中画出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程kx2﹣2(k+1)x+k﹣1=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)是否存在实数k,使![]() =1成立?若存在,请求出k的值;若不存在,请说明理由.
=1成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,请将下列过程补充完整:
收集数据:
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:

整理、描述数据:
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70—79分为生产技能良好,60—69分为生产技能合格,60分以下为生产技能不合格)
分析数据:
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | |
乙 | 78 | 81 |
得出结论:
![]() .估计乙部门生产技能优秀的员工人数约为 .
.估计乙部门生产技能优秀的员工人数约为 .
![]() .可以推断出 部门员工的生产技能水平高.理由为 .
.可以推断出 部门员工的生产技能水平高.理由为 .
(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中仅有2个红球、1个黑球,这些球除颜色外无其他差别.
(1)甲同学先随机摸出一个小球,记下颜色后放回搅匀,再随机摸出一个小球,则两次摸出的小球颜色不同的概率是多少?
(2)乙同学从中一次摸出两个球,则摸出的小球均为红色的概率是___ _.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师准备了四张背面都一样的卡片A、B、C、D,每张卡片的正面标有字母a、b、c表示三条线段(如下图).把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.

⑴ 李老师随机抽取一张卡片,抽到卡片B的概率等于 ;
⑵ 求李老师抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某班学生每天使用零花钱的情况,小明随机调查了15名同学,结果如表:
每天使用零花钱(单位:元) | 0 | 2 | 3 | 4 | 5 |
人数 | 1 | 4 | 5 | 3 | 2 |
关于这15名同学每天使用零花钱的情况,下列说法正确的是( )
A.中位数是3元B.众数是5元
C.平均数是2.5元D.方差是4
查看答案和解析>>
科目:初中数学 来源: 题型:
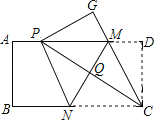
【题目】如图,先有一张矩形纸片![]() 点
点![]() 分别在矩形的边
分别在矩形的边![]() 上,将矩形纸片沿直线MN折叠,使点
上,将矩形纸片沿直线MN折叠,使点![]() 落在矩形的边
落在矩形的边![]() 上,记为点
上,记为点![]() ,点
,点![]() 落在
落在![]() 处,连接
处,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:
.下列结论:
![]()
②四边形![]() 是菱形;
是菱形;
③![]() 重合时,
重合时,![]() ;
;
④![]() 的面积
的面积![]() 的取值范围是
的取值范围是![]()
其中正确的是_____(把正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
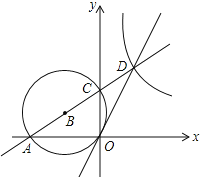
【题目】如图,在平面直角坐标系中,半径为![]() 的⊙B经过原点O,且与x,y轴分交于点A,C,点C的坐标为(0,2),AC的延长线与⊙B的切线OD交于点D,则经过D点的反比例函数的解析式为_______.
的⊙B经过原点O,且与x,y轴分交于点A,C,点C的坐标为(0,2),AC的延长线与⊙B的切线OD交于点D,则经过D点的反比例函数的解析式为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com