
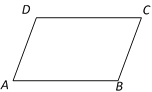
【题目】已知:在平行四边形ABCD中,AB︰BC=3︰2.
(1)根据条件画图:作∠BCD的平分线,交边AB于点E,取线段BE的中点F,连接DF交CE于点G.
(2)设![]() ,那么向量
,那么向量![]() =______.(用向量
=______.(用向量![]() 、
、![]() 表示),并在图中画出向量
表示),并在图中画出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
科目:初中数学 来源: 题型:
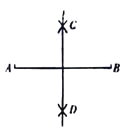
【题目】阅读下面材料:在教学课上,老师提出如下问题:尺规作图:作一条线段的垂直平分线.
已知:线段AB.
![]()
求作:线段AB的垂直平分线.
小芸的作法如下:如图, (1)分别以点A和点B为圆心,大于![]() 的长为半径作弧,两孤相交于C,D两点; (2)作直线CD.所以直线CD就是所求作的垂直平分线.
的长为半径作弧,两孤相交于C,D两点; (2)作直线CD.所以直线CD就是所求作的垂直平分线.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是____________________,
查看答案和解析>>
科目:初中数学 来源: 题型:
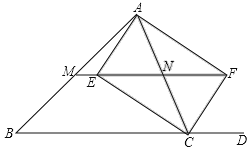
【题目】如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
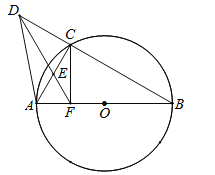
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
(2)若DA=![]() AF,求证:CF⊥AB.
AF,求证:CF⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P(﹣1,m)是双曲线y=![]() 上的一个点,过点P作PQ⊥x轴于点Q,连接PO,△OPQ的面积为3.
上的一个点,过点P作PQ⊥x轴于点Q,连接PO,△OPQ的面积为3.

(1)求m的值和双曲线对应的函数表达式;
(2)若经过点P的一次函数y=kx+b(k≠0、b≠0)的图象与x轴交于点A,与y交于点B且PB=2AB,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座人行天桥示意图,天桥离地面的高BC是10m,坡面AC的倾斜角∠CAB=45°,在距离A点12m处有一建筑物HQ.为方便行人过天桥,市政部门决定降低坡度,使新坡面CD的倾斜角∠CDB=37°,若新坡面下D处需留至少4m人行道,则该建筑物HQ是否需要拆除?请通过计算说明理由.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
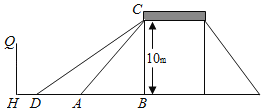
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、CEFG都是正方形,E在CD上且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,下列四个结论:
① BE⊥GD; ② OH=![]() BG; ③ ∠AHD=45°; ④ GD=
BG; ③ ∠AHD=45°; ④ GD=![]() AM.
AM.
其中正确的结论个数有

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com