
【题目】如图,![]() 内接于⊙
内接于⊙![]() ,
,![]() ,
,![]() ∥
∥![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
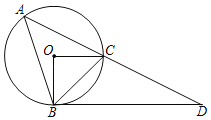
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,
,![]() .
.
①求![]() 的度数;
的度数;
②求![]() 的长.
的长.
【答案】(1)详见解析;(2)①![]() ;②
;②![]()
【解析】
(1)由![]() ,得到∠O=90°,由
,得到∠O=90°,由![]() ∥
∥![]() 得到∠ODB=∠O,根据切线的判定定理得到结论;
得到∠ODB=∠O,根据切线的判定定理得到结论;
(2)①先求出∠CBD和∠ACB的度数,即可求出![]() 的度数;
的度数;
②如图,过点C分别作CF⊥AB,CE⊥BD, 先求出CD和AC的长,再求![]() 的长即可.
的长即可.
解:(1)证明:∵∠BAC=45°,
∴∠BOC=2∠BAC=90°,
∵BD∥OC,
∴∠BOC+∠OBD=180°,
∴∠OBD=90°,
∴BD是⊙O的切线;
(2)①∵OC=OB,∠O=90°,
∴∠OBC=∠OCB=45°,
∵∠OBD=90°,
∴∠CBD=45°,
∵![]() ,
,
∴∠ABC=60°
在△ABC中,![]() ,∠ABC=60°
,∠ABC=60°
∴∠ACB=75°,
∴∠D=∠ACB-∠CBD=75°-45°=30°;
②如图,过点C分别作CF⊥AB于点F,CE⊥BD于点E,
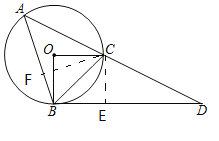
∵∠OBC=45°, ![]() ,
,
∴CE=BC·sin∠CBE=2,
∵∠D=30°,
∴CD=2CE=4,
在△FBC中,∠FBC=60°, ![]() ,
,
∴CF=BC·sin∠CBF=![]() ,
,
在△ACF中,∠A=45°,
∴AC=![]() =
=![]() ,
,
∴AD=AC+CD=![]() .
.


科目:初中数学 来源: 题型:
【题目】为了解我县中学生参加“新冠肺炎知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,根据成绩分成如下四个组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,并制作出如下的扇形统计图和直方图.请根据图表信息解答下列问题:
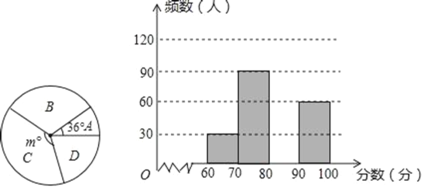
(1)扇形统计图中的m= ,并在图中补全频数分布直方图;
(2)小明的成绩是所有被抽查学生成绩的中位数 ,据此推断他的成绩在 组;
(3)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A,C两组学生的概率是多少?请列表或画树状图说明;
(4)若我县学生人数为18000人,请根据上述调查结果,估计我县学生成绩在C、D两组的共多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
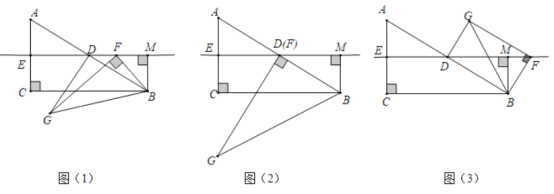
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,过点
的中点,过点![]() 作直线
作直线![]() 的垂线段
的垂线段![]() 垂足为
垂足为![]() .点
.点![]() 是直线
是直线![]() 上一动点,作
上一动点,作![]() 使
使![]() ,
,![]() 连接
连接![]() .
.
(1)观察猜想:如图(2),当点![]() 与点
与点![]() 重合时,则
重合时,则![]() 的值为 .
的值为 .
(2)问题探究:如图(1),当点![]() 与点
与点![]() 不重合时,请求出
不重合时,请求出![]() 的值及两直线
的值及两直线![]() 夹角锐角的度数,并说明理由
夹角锐角的度数,并说明理由
(3)问题解决:如图(3),当点![]() 在同一直线上时,请直接写出
在同一直线上时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
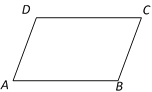
【题目】已知:在平行四边形ABCD中,AB︰BC=3︰2.
(1)根据条件画图:作∠BCD的平分线,交边AB于点E,取线段BE的中点F,连接DF交CE于点G.
(2)设![]() ,那么向量
,那么向量![]() =______.(用向量
=______.(用向量![]() 、
、![]() 表示),并在图中画出向量
表示),并在图中画出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产的甲、乙两种产品,已知2件甲商品的出厂总价与3件乙商品的出厂总价相同,3件甲商品的出厂总价比2件乙商品的出厂总价多1500元.
(1)求甲、乙商品的出厂单价分别是多少?
(2)某销售商计划购进甲商品200件,购进乙商品的数量是甲的4倍.恰逢该厂正在对甲商品进行降价促销活动,甲商品的出厂单价降低了![]() ,该销售商购进甲的数量比原计划增加了
,该销售商购进甲的数量比原计划增加了![]() ,乙的出厂单价没有改变,该销售商购进乙的数量比原计划少了
,乙的出厂单价没有改变,该销售商购进乙的数量比原计划少了![]() .结果该销售商付出的总货款与原计划的总货款恰好相同,求
.结果该销售商付出的总货款与原计划的总货款恰好相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉某超市在疫情前用3000元购进某种干果销售,发生疫情后,为了保障附近居民的生活需求,又调拨9000元购进该种干果.受疫情影响,交通等成本上涨,第二次的进价比第一次进价提高了20%,但是第二次购进干果的数量是第一次的2倍还多300千克,如果超市先按每千克9元的价格出售,当大部分干果售出后,最后的600千克按原售价的7折售完.售卖结束后,超市决定将盈利的资金捐助给武汉市用于抗击新冠肺炎疫情.那么该超市可以捐助___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .
.
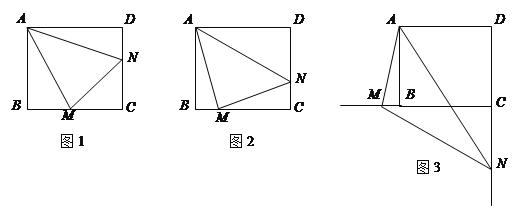
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),线段
时(如图2),线段![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当![]() 绕点
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() 和
和![]() 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程kx2﹣2(k+1)x+k﹣1=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)是否存在实数k,使![]() =1成立?若存在,请求出k的值;若不存在,请说明理由.
=1成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某班学生每天使用零花钱的情况,小明随机调查了15名同学,结果如表:
每天使用零花钱(单位:元) | 0 | 2 | 3 | 4 | 5 |
人数 | 1 | 4 | 5 | 3 | 2 |
关于这15名同学每天使用零花钱的情况,下列说法正确的是( )
A.中位数是3元B.众数是5元
C.平均数是2.5元D.方差是4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com