
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .
.
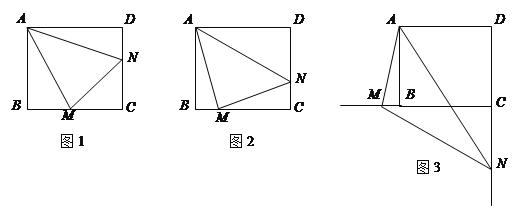
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),线段
时(如图2),线段![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当![]() 绕点
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() 和
和![]() 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.
【答案】(1)![]() ,证明见解析(2)
,证明见解析(2)![]()
【解析】
(1)BM+DN=MN成立,证得B、E、M三点共线即可得到△AEM≌△ANM,从而证得ME=MN.
(2)DN-BM=MN.证明方法与(1)类似.
(1)BM+DN=MN成立.
证明:如图,把△ADN绕点A顺时针旋转90°,得到△ABE,则可证得E、B、M三点共线.

∴∠EAM=90°-∠NAM=90°-45°=45°,
又∵∠NAM=45°,
∴在△AEM与△ANM中,
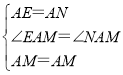
∴△AEM≌△ANM(SAS),
∴ME=MN,
∵ME=BE+BM=DN+BM,
∴DN+BM=MN;
(2)DN-BM=MN.
在线段DN上截取DQ=BM,如图,
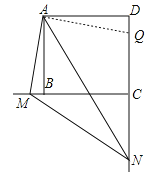
在△ADQ与△ABM中,
∵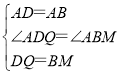 ,
,
∴△ADQ≌△ABM(SAS),
∴∠DAQ=∠BAM,
∴∠QAN=∠MAN.
在△AMN和△AQN中,
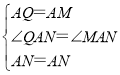
∴△AMN≌△AQN(SAS),
∴MN=QN,
∴DN-BM=MN.


科目:初中数学 来源: 题型:
【题目】世界卫生组织通报说,沙特阿拉伯报告新增5例中东呼吸系统综合征冠状病毒(新型冠状病毒)确诊病例.全球新型冠状病毒确诊病例已达176例,其中死亡74例.冠状病毒颗粒的直径60-200nm,平均直径为100nm,新型冠状病毒直径为178nm,呈球形或椭圆形,具有多形性.如果1nm=10-9米,那么新型冠状病毒的半径约为( )米
A.1.00×10-7B.1.78×10-7C.8.90×10-8D.5.00×10-8
查看答案和解析>>
科目:初中数学 来源: 题型:
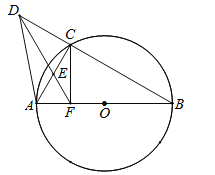
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
(2)若DA=![]() AF,求证:CF⊥AB.
AF,求证:CF⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
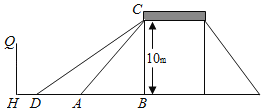
【题目】如图,是一座人行天桥示意图,天桥离地面的高BC是10m,坡面AC的倾斜角∠CAB=45°,在距离A点12m处有一建筑物HQ.为方便行人过天桥,市政部门决定降低坡度,使新坡面CD的倾斜角∠CDB=37°,若新坡面下D处需留至少4m人行道,则该建筑物HQ是否需要拆除?请通过计算说明理由.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+4![]() ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+![]() ,其中正确的结论是( )
,其中正确的结论是( )

A. ①②③⑤ B. ①②③④ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() .
.
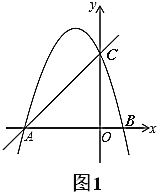
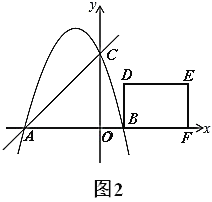
(1)求抛物线表达式;
(2)在第二象限的抛物线上有一点![]() ,且点
,且点![]() 到线段
到线段![]() 的距离为
的距离为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)矩形![]() 的边
的边![]() 在
在![]() 轴的正半轴,
轴的正半轴,![]() 在第一象限,
在第一象限,![]() ,
,![]() ,将矩形
,将矩形![]() 沿
沿![]() 轴负方向平移
轴负方向平移![]()
![]() ,直线
,直线![]() 、
、![]() 分别交抛物线于
分别交抛物线于![]() 、
、![]() .问:是否存在实数
.问:是否存在实数![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请直接写出
为顶点的四边形是平行四边形?若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一个面积为150平方米的长方形养鸡场,鸡场的一边靠墙(墙长18米),另三边用竹篱笆围成,在与墙平行的一边,开一扇2米宽的门.如果竹篱笆的长为33米,求这个长方形养鸡场与墙垂直的边长是多少?与墙平行的边长是多少?(列方程解答)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com