
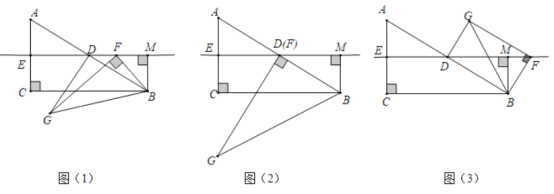
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,过点
的中点,过点![]() 作直线
作直线![]() 的垂线段
的垂线段![]() 垂足为
垂足为![]() .点
.点![]() 是直线
是直线![]() 上一动点,作
上一动点,作![]() 使
使![]() ,
,![]() 连接
连接![]() .
.
(1)观察猜想:如图(2),当点![]() 与点
与点![]() 重合时,则
重合时,则![]() 的值为 .
的值为 .
(2)问题探究:如图(1),当点![]() 与点
与点![]() 不重合时,请求出
不重合时,请求出![]() 的值及两直线
的值及两直线![]() 夹角锐角的度数,并说明理由
夹角锐角的度数,并说明理由
(3)问题解决:如图(3),当点![]() 在同一直线上时,请直接写出
在同一直线上时,请直接写出![]() 的值.
的值.
【答案】(1)2;(2)60°,见解析;(3)4+![]() 或4-
或4-![]()
【解析】
(1)由题意可知结论为当点F与点D重合时,则![]() 的值为2,并根据题意设BM=a,求出DM,GD即可解决问题;
的值为2,并根据题意设BM=a,求出DM,GD即可解决问题;
(2)由题意可知结论为![]() 的值为2,两直线GD、ED夹角锐角的度数为60°,并利用全等三角形的判定定理证明△BGD∽△BFM,可得结论;
的值为2,两直线GD、ED夹角锐角的度数为60°,并利用全等三角形的判定定理证明△BGD∽△BFM,可得结论;
(3)根据题意分两种情形:当点G在线段AF上时以及当点G在线段AF的延长线上时,分别进行求解即可.
解:(1) 设BM=a.
∵AE=EC,AD=DB,
∴DE∥BC,
∴∠BDM=∠ABC=30°,
∵BM⊥EM,
∴∠BMD=90°,
∴![]() ,
,
在Rt△GDB中,∵∠GDB=90°,∠G=30°,
∴![]() ,
,
∴![]() .
.
故答案为:2.
(2)在Rt△BDM中,设BM=a,则BD=2a,DM=![]() a
a
在Rt△BGF中,设BF=b,则BG=2b,FG=![]()
在△BGD与△BFM中,
∵BG:BF=2b:b=2a:a=BF:BM,∠DBG=60°-∠FBD=∠FBM
∴△BGD∽△BFM
则DG:FM=BD:BM=2a:a=2:1
即![]() 的值为2.
的值为2.
如图,延长GD、BF交于点P,
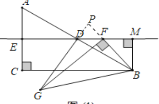
∵△BGD∽△BFM
∴∠PFD=∠MFB=∠BGD
则在△PDF与△PBG中,∠PDF=∠PBG=60°.
故![]() 的值为2,两直线GD、ED夹角锐角的度数为60°.
的值为2,两直线GD、ED夹角锐角的度数为60°.
(3)如图,有以下两种如图3①,图3②
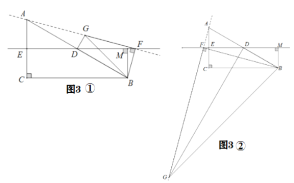
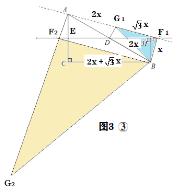
如图3③,ED是△ABC的中垂线;
∵在Rt△AF1B和Rt△AF2B中,DA=DF1=DF2=DB
∴四边形AF2BF1是矩形
当点G在线段AF上时,在Rt△BF1G1中,
设BF1=x,则BG1=2x=AG1,F1G1=![]()
∴BG1:AF1=![]() :
:![]() =4-
=4-![]()
当点G在线段AF的延长线上时,在矩形AF2BF1中,
设AF2=BF1=x, F2B=AF1=![]()
∴BG2=2![]()
则BG2:AF2=2![]() :x=4+
:x=4+![]() .
.
∴![]() 的值为4+
的值为4+![]() 或4-
或4-![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
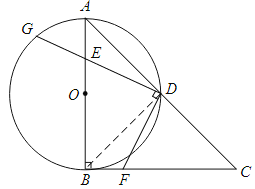
【题目】如图,在RtΔABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接EF,求证:∠FEB=∠GDA;
(3)连接GF,若AE=2,EB=4,求ΔGFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界卫生组织通报说,沙特阿拉伯报告新增5例中东呼吸系统综合征冠状病毒(新型冠状病毒)确诊病例.全球新型冠状病毒确诊病例已达176例,其中死亡74例.冠状病毒颗粒的直径60-200nm,平均直径为100nm,新型冠状病毒直径为178nm,呈球形或椭圆形,具有多形性.如果1nm=10-9米,那么新型冠状病毒的半径约为( )米
A.1.00×10-7B.1.78×10-7C.8.90×10-8D.5.00×10-8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:在教学课上,老师提出如下问题:尺规作图:作一条线段的垂直平分线.
已知:线段AB.
![]()
求作:线段AB的垂直平分线.
小芸的作法如下:如图, (1)分别以点A和点B为圆心,大于![]() 的长为半径作弧,两孤相交于C,D两点; (2)作直线CD.所以直线CD就是所求作的垂直平分线.
的长为半径作弧,两孤相交于C,D两点; (2)作直线CD.所以直线CD就是所求作的垂直平分线.
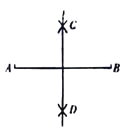
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是____________________,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年全国两会于3月5日在人民大会堂开幕,某社区为了解居民对此次两会的关注程度,在全社区范围内随机抽取部分居民进行问卷调查,根据调查结果,把居民对两会的关注程度分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下不完整的统计图:
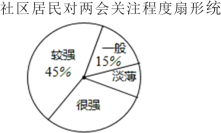
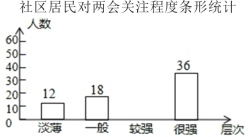
请结合图表中的信息,解答下列问题:
(1)此次调查一共随机抽取了_____名居民;
(2)请将条形统计图补充完整;
(3)扇形统计图中,“很强”所对应扇形圆心角的度数为_____;
(4)若该社区有1500人,则可以估计该社区居民对两会的关注程度为“淡薄”层次的约有 _____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
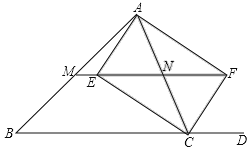
【题目】如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
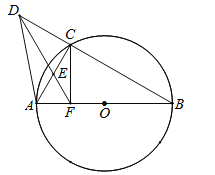
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
(2)若DA=![]() AF,求证:CF⊥AB.
AF,求证:CF⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() .
.
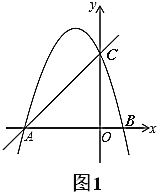
(1)求抛物线表达式;
(2)在第二象限的抛物线上有一点![]() ,且点
,且点![]() 到线段
到线段![]() 的距离为
的距离为![]() ,求点
,求点![]() 的坐标;
的坐标;
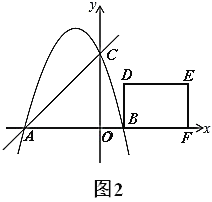
(3)矩形![]() 的边
的边![]() 在
在![]() 轴的正半轴,
轴的正半轴,![]() 在第一象限,
在第一象限,![]() ,
,![]() ,将矩形
,将矩形![]() 沿
沿![]() 轴负方向平移
轴负方向平移![]()
![]() ,直线
,直线![]() 、
、![]() 分别交抛物线于
分别交抛物线于![]() 、
、![]() .问:是否存在实数
.问:是否存在实数![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请直接写出
为顶点的四边形是平行四边形?若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com