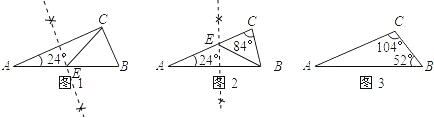
【题目】（1）如图1,△ABC中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,但须保留作图痕迹).
（2）已知内角度数的两个三角形如图2,图3所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.
【答案】（1）见解析；（2）图2能画一条直线分割成两个等腰三角形，分割成的两个等腰三角形的顶角分别是132°和84°；图3不能分割成两个等腰三角形.
【解析】
（1）本题中，只要找到斜边中点，然后连接直角顶点和斜边中点，那么分成的两个三角形就是等腰三角形．那么只要作AC的垂直平分线就可以了．AC的垂直平分线与AB的交点就是AB的中点；
（2）本题要先根据三角形的内角和求出另一角的度数，然后看看是否能分成等腰三角形．
图2可以将∠B分成24°和48°．图3不能分成等腰三角形．
（1）如图,直线CE即为所求；
（2）图2能画一条直线分割成两个等腰三角形,
分割成的两个等腰三角形的顶角分别是132°和84°.
图3不能分割成两个等腰三角形.
科目：初中数学 来源： 题型：
【题目】已知平面上点
，
，
，
（每三点都不在一条直线上）.
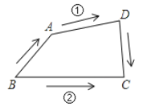
（1）经过这四点最多能确定 条直线.
（2）如图这四点表示公园四个地方，如果点，在公园里湖对岸两处，，在湖面上，要从到筑桥，从节省材料的角度考虑，应选择图中两条路中的哪一条？如果有人想在桥上较长时间观赏湖面风光，应选择哪一条？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，数轴上A、B两点分别对应有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB＝|a﹣b|，利用数形结合思想回答下列问题：
(1)数轴上表示2和10两点之间的距离是_______.
(2)数轴上一个点到表示2的点的距离为5.2，这个点表示的数为______.
(3)若x表示一个数，数轴上表示x和﹣5的两点之间的距离是____；(用含x的式子表示)
(4)若x表示一个数，|x+1|+|x﹣2|的最小值是______，相应的x的取值范围_______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】快车和慢车分别从甲、乙两地同时出发，匀速相向而行，快车到达乙地后，慢车继续前行，设出发
小时后，两车相距
千米，图中折线表示从两车出发至慢车到达甲地的过程中与之间的函数关系式，根据图中信息，解答下列问题.
（1）甲、乙两地相距 千米，快车从甲地到乙地所用的时间是 小时；
（2）求线段
的函数解析式（写出自变量取值范围），并说明点
的实际意义.
（3）求快车和慢车的速度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图，两个圈分别表示负数集和分数集. 请你把下列各数填入表示它所在的数集的圈里：
-50% ， 2011 ， 0.618 ， -3 ，
，0 ， 5.9，-3.14 ， -92 .
（2）图中，这两个圈的重叠部分表示什么数的集合？
（3）在（1）的数据中，求最大的数与最小的数之和.
查看答案和解析>>
科目：初中数学 来源： 题型：
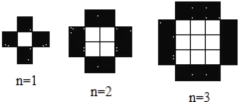
【题目】当
等于
,
,
，
时，由白色小正方形和黑色小正方形组成的图形分别如图所示.则第个图形中白色小正方形和黑色小正方形的个数总和等于，___________.（用表示，是正整数）
查看答案和解析>>
科目：初中数学 来源： 题型：
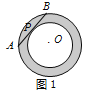
【题目】（1）如图1，同心圆中，大圆O的弦AB与小圆O切于点P，且AB=16，则圆环面积为________；
（2）如图2，同心圆中，大圆O的弦AB与小圆O相交，其中一个交点为点P，且AP=2，PB=8，则圆环面积为________.
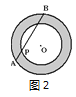
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,
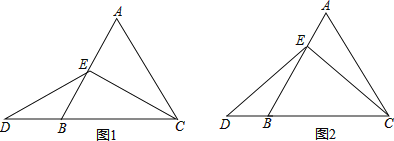
（1）当点E为AB的中点时,如图1,求证:EC=ED;
（2）当点E不是AB的中点时,如图2,过点E作EF//BC,求证:△AEF是等边三角形;
（3）在第(2)小题的条件下,EC与ED还相等吗,请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把下列各数前的序号分别填入相应的集合内：
①－2.5， ②0，③
，④
，⑤
，⑥
，⑦－0.5252252225…(每两个5之间依次增加1个2）．
（1）正数集合： { …}；
（2）负分数集合：{ …}；
（3）整数集合： { …}；
（4）无理数集合：{ …}．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com