
【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,利用数形结合思想回答下列问题:
(1)数轴上表示2和10两点之间的距离是_______.
(2)数轴上一个点到表示2的点的距离为5.2,这个点表示的数为______.
(3)若x表示一个数,数轴上表示x和﹣5的两点之间的距离是____;(用含x的式子表示)
(4)若x表示一个数,|x+1|+|x﹣2|的最小值是______,相应的x的取值范围_______.
![]()
【答案】(1)8;(2)7.2或﹣3.2;(3)|x+5|;(4)3,﹣1≤x≤2.
【解析】
(1)根据题目中的数据,可以计算出这两个数之间的距离;
(2)根据数轴上一个点到表示2的点的距离为5.2,可以求得这个点表示的数;
(3)根据题意,可以用含x的代数式表示出x和﹣5的两点之间的距离;
(4)利用分类讨论的方法可以解答本题.
(1)数轴上表示2和10两点之间的距离是10﹣2=8,
故答案为:8;
(2)数轴上一个点到表示2的点的距离为5.2,这个点表示的数为:2+5.2=7.2或2﹣5.2=﹣3.2,
故答案为:7.2或﹣3.2;
(3)数轴上表示x和﹣5的两点之间的距离是:|x﹣(﹣5)|=|x+5|,
故答案为:|x+5|;
(4)当x>2时,|x+1|+|x﹣2|=x+1+x﹣2=2x﹣1>3,
当﹣1≤x≤2时,|x+1|+|x﹣2|=x+1+2﹣x=3,
当x<﹣1时,|x+1|+|x﹣2|=﹣x﹣1+2﹣x=﹣2x+1>3,
由上可得,|x+1|+|x﹣2|的最小值是3,
故答案为:3,﹣1≤x≤2.


科目:初中数学 来源: 题型:
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,则图3中共有7个正方形;……如此剪下去,则第n个图形中正方形的个数是多少?

(1)将下表填写完整:
图(n) | 1 | 2 | 3 | 4 | 5 | …… | n |
正方形的个数 | 1 | 4 | 7 | …… | an |
(2)an= (用含n的代数式表示)
(3)按照上述方法,能否得到2019个正方形?如果能,请求出n;如果不能,请简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
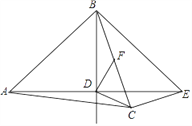
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,线段
,线段![]() .
.
(1)如图,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,则线段
的中点,则线段![]() 的长度是 ;
的长度是 ;
![]()
(2)若把(1)中点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,改为点
,改为点![]() 是线段
是线段![]() 上任意一点,且
上任意一点,且![]() ,
,![]() ,其他条件不变,请求出线段
,其他条件不变,请求出线段![]() 的长度(用含
的长度(用含![]() 、
、![]() 的式子表示);
的式子表示);
(3)若把(2)中点![]() 是线段
是线段![]() 上任意一点,改为点
上任意一点,改为点![]() 是直线
是直线![]() 上任意一点,其他条件不变,则线段
上任意一点,其他条件不变,则线段![]() 的长度会变化吗?若有变化,求出结果.
的长度会变化吗?若有变化,求出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的平分线”的是( )
A. ∠AOC=∠BOC B. ∠AOB=2∠BOC
C. ∠AOC=![]() ∠AOB D. ∠AOC+∠BOC=∠AOB
∠AOB D. ∠AOC+∠BOC=∠AOB
查看答案和解析>>
科目:初中数学 来源: 题型:
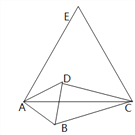
【题目】如图,四边形ABCD中,AD//BC,AD=AB=2,∠B=120°,∠ADC=150°,现以对角线AC为边向点D一侧作等边△ACE,则四边形ABCE的面积=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD 中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N ,连接OM,ON,MN .下列五个结论:①△CNB≌△DMC ;②△CON≌△DOM ;③△OMN≌△OAD ;④![]() ;⑤若AB=2,则
;⑤若AB=2,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,但须保留作图痕迹).
(2)已知内角度数的两个三角形如图2,图3所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AD=6,DC=7,点H为AD上一点,并且AH=2,点E为AB上一动点,以HE为边长作菱形HEFG,并且使点G在CD边上,连接CF
(1)如图1,当DG=2时,求证:四边形EFGH为正方形;
(2)如图2,当DG=6时,求△CGF的面积;
(3)当DG的长度为何值时,△CGF的面积最小,并求出△CGF面积的最小值;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com