
【题目】已知点![]() ,线段
,线段![]() .
.
(1)如图,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,则线段
的中点,则线段![]() 的长度是 ;
的长度是 ;
![]()
(2)若把(1)中点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,改为点
,改为点![]() 是线段
是线段![]() 上任意一点,且
上任意一点,且![]() ,
,![]() ,其他条件不变,请求出线段
,其他条件不变,请求出线段![]() 的长度(用含
的长度(用含![]() 、
、![]() 的式子表示);
的式子表示);
(3)若把(2)中点![]() 是线段
是线段![]() 上任意一点,改为点
上任意一点,改为点![]() 是直线
是直线![]() 上任意一点,其他条件不变,则线段
上任意一点,其他条件不变,则线段![]() 的长度会变化吗?若有变化,求出结果.
的长度会变化吗?若有变化,求出结果.
【答案】(1)10;(2)![]() ;(3)线段
;(3)线段![]() 的长度会变化,
的长度会变化,![]() 或
或![]() 或
或![]()
【解析】
(1)根据中点的定义求出MC、NC的长,相加即可;
(2)根据中点的定义用含有a、b的式子出MC、NC的长,相加即可;
(3)根据中点的定义用含有a、b的式子出MC、NC的长,分当点![]() 在线段
在线段![]() 上时、当点
上时、当点![]() 在线段
在线段![]() 上的延长线时、当点
上的延长线时、当点![]() 在线段
在线段![]() 上的延长线时三种情况讨论.
上的延长线时三种情况讨论.
(1)由点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() ,
,![]()
可得![]() ,
,![]()
所以![]()
故答案为:10
(2)由点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点
的中点
可得![]() ,
,![]()
所以![]()
(3)线段![]() 的长度会变化
的长度会变化
当点![]() 在线段
在线段![]() 上时,由(2)知
上时,由(2)知![]()
当点![]() 在线段
在线段![]() 上的延长线时,如图,
上的延长线时,如图,
![]()
则![]() ,即
,即![]()
由点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点
的中点
可得![]() ,
,![]()
所以![]()
当点![]() 在线段
在线段![]() 上的延长线时,如图
上的延长线时,如图
![]()
则![]() ,即
,即![]()
由点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点
的中点
可得![]() ,
,![]()
所以![]()


科目:初中数学 来源: 题型:
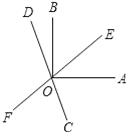
【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面上点![]() ,
,![]() ,
,![]() ,
,![]() (每三点都不在一条直线上).
(每三点都不在一条直线上).
(1)经过这四点最多能确定 条直线.
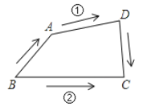
(2)如图这四点表示公园四个地方,如果点![]() ,
,![]() 在公园里湖对岸两处,
在公园里湖对岸两处,![]() ,
,![]() 在湖面上,要从
在湖面上,要从![]() 到
到![]() 筑桥,从节省材料的角度考虑,应选择图中两条路中的哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?
筑桥,从节省材料的角度考虑,应选择图中两条路中的哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的和距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯,建立适当坐标系.
(1)求抛物线的解析式.
(2)求两盏景观灯之间的水平距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将若干个奇数按每行8个数排成如图的形式:
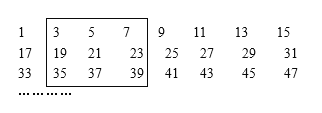
小军画了一方框框住了其中的9个数.
(1)如图中方框内9个数之和是 ;
(2)若小军画的方框内9个数之和等于333,则这个方框内左下角的那个数为_________;
(3)试说明:方框内的9个数之和总是9的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前我市“校园手机”现象越来越受到社会关注,针对这种现象,我市某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的看法,统计整理并制作了如下的统计图:
(1)这次调查的家长总数为________人.家长表示“不赞同”的人数为________人;
(2)请在图①中把条形统计图补充完整;
(3)从这次接受调查的家长中随机抽查一个,恰好是“赞同”的家长的概率是________;
(4)求图②中表示家长“无所谓”的扇形圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,利用数形结合思想回答下列问题:
(1)数轴上表示2和10两点之间的距离是_______.
(2)数轴上一个点到表示2的点的距离为5.2,这个点表示的数为______.
(3)若x表示一个数,数轴上表示x和﹣5的两点之间的距离是____;(用含x的式子表示)
(4)若x表示一个数,|x+1|+|x﹣2|的最小值是______,相应的x的取值范围_______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车和慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后,慢车继续前行,设出发![]() 小时后,两车相距
小时后,两车相距![]() 千米,图中折线表示从两车出发至慢车到达甲地的过程中
千米,图中折线表示从两车出发至慢车到达甲地的过程中![]() 与
与![]() 之间的函数关系式,根据图中信息,解答下列问题.
之间的函数关系式,根据图中信息,解答下列问题.
(1)甲、乙两地相距 千米,快车从甲地到乙地所用的时间是 小时;
(2)求线段![]() 的函数解析式(写出自变量取值范围),并说明点
的函数解析式(写出自变量取值范围),并说明点![]() 的实际意义.
的实际意义.
(3)求快车和慢车的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,
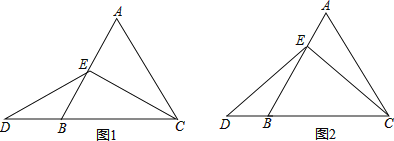
(1)当点E为AB的中点时,如图1,求证:EC=ED;
(2)当点E不是AB的中点时,如图2,过点E作EF//BC,求证:△AEF是等边三角形;
(3)在第(2)小题的条件下,EC与ED还相等吗,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com