
【题目】快车和慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后,慢车继续前行,设出发![]() 小时后,两车相距
小时后,两车相距![]() 千米,图中折线表示从两车出发至慢车到达甲地的过程中
千米,图中折线表示从两车出发至慢车到达甲地的过程中![]() 与
与![]() 之间的函数关系式,根据图中信息,解答下列问题.
之间的函数关系式,根据图中信息,解答下列问题.
(1)甲、乙两地相距 千米,快车从甲地到乙地所用的时间是 小时;
(2)求线段![]() 的函数解析式(写出自变量取值范围),并说明点
的函数解析式(写出自变量取值范围),并说明点![]() 的实际意义.
的实际意义.
(3)求快车和慢车的速度.

【答案】(1)640,6.4;(2)y=-160x+640,自变量取值范围是0≤x≤4,Q点为快车与慢车相遇的时间;(3)快车速度:100千米/时;慢车速度:60千米/时.
【解析】
PQ段的速度表示两车速度和,在Q点表示两车相遇,M点表示快车已经到达了乙地,MN表示只有慢车还在行驶
(1)直接由图像即可得到结果 (2)利用P点和(![]() ,440)可求出直线PQ的解析式,然后求出Q点,自变量的取值范围即从0到Q的横坐标 (3)由PQ直线算出速度和,由第一问得到快车的速度,然后得到慢车速度即可
,440)可求出直线PQ的解析式,然后求出Q点,自变量的取值范围即从0到Q的横坐标 (3)由PQ直线算出速度和,由第一问得到快车的速度,然后得到慢车速度即可
(1)由图像可知,两车未出发时两车最远,即甲乙两地的距离为640km;由图像可知在6.4小时之后只有慢车还在运动,所以快车从甲地到达乙地的时间为6.4小时
(2)因为P点坐标为(0,640),所以可设PQ直线解析式为y=kx+640,将点(![]() ,440)代入,得到方程440=
,440)代入,得到方程440=![]() k+640,解得k=-160,所以PQ函数解析式为y=-160x+640;Q点的坐标为(4,0),所以线段PQ函数解析式的自变量取值范围是0≤x≤4,Q点的意义是快车与慢车相遇的时间
k+640,解得k=-160,所以PQ函数解析式为y=-160x+640;Q点的坐标为(4,0),所以线段PQ函数解析式的自变量取值范围是0≤x≤4,Q点的意义是快车与慢车相遇的时间
(3)由PQ段可得到两车的速度和为(640-440)÷![]() =160km/h,由(1)可得到快车的速度为640÷6.4=100km/h,则慢车速度为60km/h
=160km/h,由(1)可得到快车的速度为640÷6.4=100km/h,则慢车速度为60km/h


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的![]() ;
;
(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,线段
,线段![]() .
.
(1)如图,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,则线段
的中点,则线段![]() 的长度是 ;
的长度是 ;
![]()
(2)若把(1)中点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,改为点
,改为点![]() 是线段
是线段![]() 上任意一点,且
上任意一点,且![]() ,
,![]() ,其他条件不变,请求出线段
,其他条件不变,请求出线段![]() 的长度(用含
的长度(用含![]() 、
、![]() 的式子表示);
的式子表示);
(3)若把(2)中点![]() 是线段
是线段![]() 上任意一点,改为点
上任意一点,改为点![]() 是直线
是直线![]() 上任意一点,其他条件不变,则线段
上任意一点,其他条件不变,则线段![]() 的长度会变化吗?若有变化,求出结果.
的长度会变化吗?若有变化,求出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
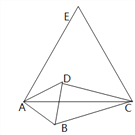
【题目】如图,四边形ABCD中,AD//BC,AD=AB=2,∠B=120°,∠ADC=150°,现以对角线AC为边向点D一侧作等边△ACE,则四边形ABCE的面积=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD 中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N ,连接OM,ON,MN .下列五个结论:①△CNB≌△DMC ;②△CON≌△DOM ;③△OMN≌△OAD ;④![]() ;⑤若AB=2,则
;⑤若AB=2,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,但须保留作图痕迹).
(2)已知内角度数的两个三角形如图2,图3所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用如图所示矩形纸片的四个角都剪去一个边长为![]() 的正方形(阴影部分).并制成一个长方体纸盒。
的正方形(阴影部分).并制成一个长方体纸盒。
(1)用a,b,x表示纸片剩余部分的面积和纸盒的底面积;
(2)当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,将一个腰长为2等腰直角△BCD和直角边长为2、宽为1的直角△CED拼在一起.现将△CED绕点C顺时针旋转至△CE’D’,旋转角为a.
(1)如图(2),旋转角a=30°时,点D′到CD边的距离D’A=______.求证:四边形ACED′为矩形;
(2)如图(1),△CED绕点C顺时针旋转一周的过程中,在BC上如何取点G,使得GD’=E’D;并说明理由.
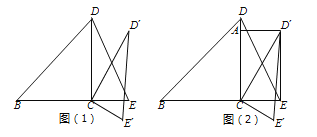
(3)△CED绕点C顺时针旋转一周的过程中,∠CE’D=90°时,直接写出旋转角a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com