
【题目】如图,在正方形ABCD 中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N ,连接OM,ON,MN .下列五个结论:①△CNB≌△DMC ;②△CON≌△DOM ;③△OMN≌△OAD ;④![]() ;⑤若AB=2,则
;⑤若AB=2,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】解:∵正方形ABCD中,CD=BC,∠BCD=90°,
∴∠BCN+∠DCN=90°,
又∵CN⊥DM,
∴∠CDM+∠DCN=90°,
∴∠BCN=∠CDM,
又∵∠CBN=∠DCM=90°,
∴△CNB≌△DMC(ASA),故①正确;
根据△CNB≌△DMC,可得CM=BN,
又∵∠OCM=∠OBN=45°,OC=OB,
∴△OCM≌△OBN(SAS),
∴OM=ON,∠COM=∠BON,
∴∠DOC+∠COM=∠COB+∠BPN,即∠DOM=∠CON,
又∵DO=CO,
∴△CON≌△DOM(SAS),故②正确;
∵∠BON+∠BOM=∠COM+∠BOM=90°,
∴∠MON=90°,即△MON是等腰直角三角形,
又∵△AOD是等腰直角三角形,
∴△OMN∽△OAD,故③正确;
∵AB=BC,CM=BN,
∴BM=AN,
又∵Rt△BMN中,BM2+BN2=MN2,
∴AN2+CM2=MN2,故④正确;
∵△OCM≌△OBN,
∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1,
∴当△MNB的面积最大时,△MNO的面积最小,
设BN=x=CM,则BM=2-x,
∴△MNB的面积=![]() x(2-x)=-
x(2-x)=-![]() x2+x,
x2+x,
∴当x=1时,△MNB的面积有最大值![]() ,
,
此时S△OMN的最小值是1-![]() =
=![]() ,故⑤正确;
,故⑤正确;
综上所述,正确结论的个数是5个,
故选:D.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线l : ![]() 经过定点P,交x、y轴于A、B两点.
经过定点P,交x、y轴于A、B两点.
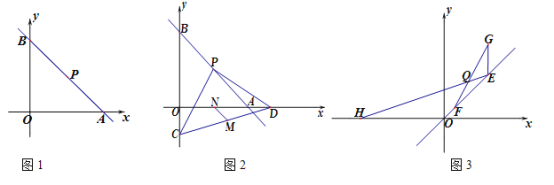
(1)如图1,直接写出点P的坐标__________________;
(2)如图2,当k=—1时,点C为y轴负半轴上一动点,过点P作PD⊥PC交x轴于点D,M、N分别为CD、OA的中点,求![]() 的值;
的值;
(3)如图3,E、F两点在射线OP上移动,EF=![]() ,点E向上移动2个单位得到点G,点E横坐标为 t(t>0),在x轴负半轴上有点H(—2t,0),FG与HE相交于Q点,求证:点Q在某条直线上运动,并求此直线的解析式.
,点E向上移动2个单位得到点G,点E横坐标为 t(t>0),在x轴负半轴上有点H(—2t,0),FG与HE相交于Q点,求证:点Q在某条直线上运动,并求此直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将若干个奇数按每行8个数排成如图的形式:
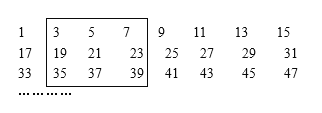
小军画了一方框框住了其中的9个数.
(1)如图中方框内9个数之和是 ;
(2)若小军画的方框内9个数之和等于333,则这个方框内左下角的那个数为_________;
(3)试说明:方框内的9个数之和总是9的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,利用数形结合思想回答下列问题:
(1)数轴上表示2和10两点之间的距离是_______.
(2)数轴上一个点到表示2的点的距离为5.2,这个点表示的数为______.
(3)若x表示一个数,数轴上表示x和﹣5的两点之间的距离是____;(用含x的式子表示)
(4)若x表示一个数,|x+1|+|x﹣2|的最小值是______,相应的x的取值范围_______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动:擦出智慧的火花---------由特殊到一般的数学思想.
数学课上,李老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC上的点,过点E作EF⊥AE,过点F作FG⊥BC交BC的延长线于点G..
(1)求证:∠BAE=∠FEG.
(2)同学们很快做出了解答,之后李老师将题目修改成:如图2,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.请借助图1完成小明的证明;
在(2)的基础上,同学们作了进一步的研究:
(3)小聪提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小聪的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车和慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后,慢车继续前行,设出发![]() 小时后,两车相距
小时后,两车相距![]() 千米,图中折线表示从两车出发至慢车到达甲地的过程中
千米,图中折线表示从两车出发至慢车到达甲地的过程中![]() 与
与![]() 之间的函数关系式,根据图中信息,解答下列问题.
之间的函数关系式,根据图中信息,解答下列问题.
(1)甲、乙两地相距 千米,快车从甲地到乙地所用的时间是 小时;
(2)求线段![]() 的函数解析式(写出自变量取值范围),并说明点
的函数解析式(写出自变量取值范围),并说明点![]() 的实际意义.
的实际意义.
(3)求快车和慢车的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,两个圈分别表示负数集和分数集. 请你把下列各数填入表示它所在的数集的圈里:
-50% , 2011 , 0.618 , -3 ,![]() ,0 , 5.9,-3.14 , -92 .
,0 , 5.9,-3.14 , -92 .

(2)图中,这两个圈的重叠部分表示什么数的集合?
(3)在(1)的数据中,求最大的数与最小的数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
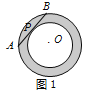
【题目】(1)如图1,同心圆中,大圆O的弦AB与小圆O切于点P,且AB=16,则圆环面积为________;
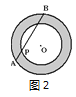
(2)如图2,同心圆中,大圆O的弦AB与小圆O相交,其中一个交点为点P,且AP=2,PB=8,则圆环面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂有甲、乙、丙三个蓄水池,已知甲蓄水池的蓄水量x是从3万吨至6万吨,乙蓄水池的蓄水量y万吨与甲蓄水池蓄水量x万吨之间的关系是: ![]() ,丙蓄水池的蓄水量的3倍恰好是甲蓄水池的蓄水量与乙蓄水池的蓄水量的积.问:
,丙蓄水池的蓄水量的3倍恰好是甲蓄水池的蓄水量与乙蓄水池的蓄水量的积.问:
(1)若丙蓄水池的蓄水量最大为22万吨,当甲蓄水池的蓄水量为6吨时, 丙蓄水池能否容纳?为什么?
(2)求丙蓄水池的蓄水量z万吨与甲蓄水池蓄水量x万吨之间的关系?
(3)蓄水池管理员在观察三个蓄水池蓄水量的记录时发现,在整个蓄水过程中, 丙蓄水池的蓄水量多次出现整数万吨的情况,你能说出共出现过多少次?分别是多少吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com